Approximating Multi-Dimensional and Multiband Signals

We study the problem of representing a discrete tensor that comes from finite uniform samplings of a multi-dimensional and multiband analog signal. Particularly, we consider two typical cases in which the shape of the subbands is cubic or parallelepipedic. For the cubic case, by examining the spectrum of its corresponding time- and band-limited operators, we obtain a low-dimensional optimal dictionary to represent the original tensor. We further prove that the optimal dictionary can be approximated by the famous \ac{dpss} with certain modulation, leading to an efficient constructing method. For the parallelepipedic case, we show that there also exists a low-dimensional dictionary to represent the original tensor. We present rigorous proof that the numbers of atoms in both dictionaries are approximately equal to the dot of the total number of samplings and the total volume of the subbands. Our derivations are mainly focused on the \ac{2d} scenarios but can be naturally extended to high dimensions.

Compressed Sensing Radar Detectors based on Weighted LASSO

The compressed sensing (CS) model can represent the signal recovery process of a large number of radar systems. The detection problem of such radar systems has been studied in many pieces of literature through the technology of debiased least absolute shrinkage and selection operator (LASSO). While naive LASSO treats all the entries equally, there are many applications in which prior information varies depending on each entry. Weighted LASSO, in which the weights of the regularization terms are tuned depending on the entry-dependent prior, is proven to be more effective with the prior information by many researchers. In the present paper, existing results obtained by methods of statistical mechanics are utilized to derive the debiased weighted LASSO estimator for randomly constructed row-orthogonal measurement matrices. Based on this estimator, we construct a detector, termed the debiased weighted LASSO detector (DWLD), for CS radar systems and prove its advantages. The threshold of this detector can be calculated by false alarm rate, which yields better detection performance than the naive weighted LASSO detector (NWLD) under the Neyman-Pearson principle. The improvement of the detection performance brought by tuning weights is demonstrated by numerical experiments. With the same false alarm rate, the detection probability of DWLD is obviously higher than those of NWLD and the debiased (non-weighted) LASSO detector (DLD).

Direction Finding in Partly Calibrated Arrays Exploiting the Whole Array Aperture

We consider the problem of direction finding using partly calibrated arrays, a distributed subarray with position errors between subarrays. The key challenge is to enhance angular resolution in the presence of position errors. To achieve this goal, existing algorithms, such as subspace separation and sparse recovery, have to rely on multiple snapshots, which increases the burden of data transmission and the processing delay. Therefore, we aim to enhance angular resolution using only a single snapshot. To this end, we exploit the orthogonality of the signals of partly calibrated arrays. Particularly, we transform the signal model into a special multiple-measurement model, show that there is approximate orthogonality between the source signals in this model, and then use blind source separation to exploit the orthogonality. Simulation and experiment results both verify that our proposed algorithm achieves high angular resolution as distributed arrays without position errors, inversely proportional to the whole array aperture.

Compressed sensing radar detectors under the row-orthogonal design model: a statistical mechanics perspective

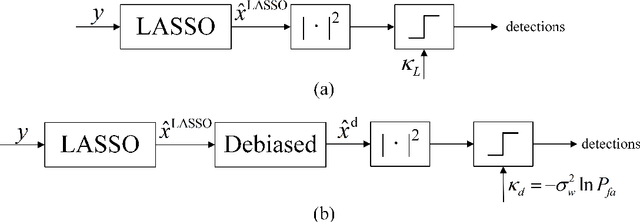
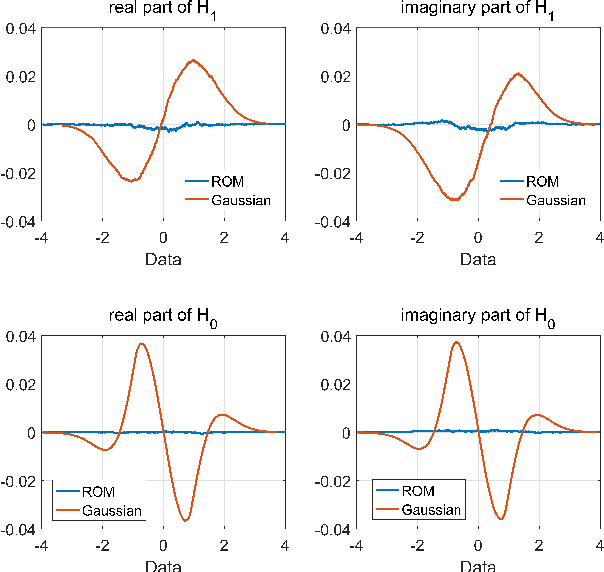
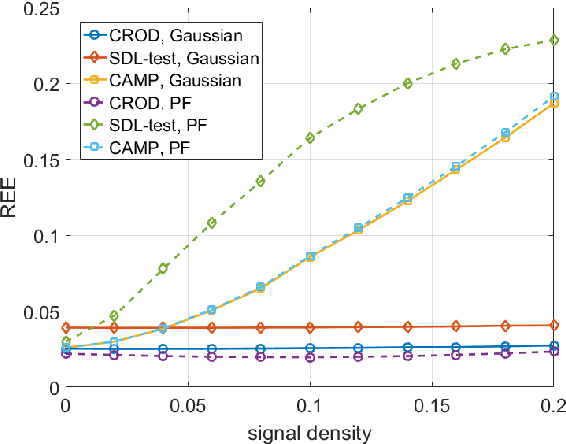
Compressed sensing (CS) model of complex-valued data can represent the signal recovery process of a large amount types of radar systems, especially when the measurement matrix is row-orthogonal. Based on debiased least absolute shrinkage and selection operator (LASSO), detection problem under Gaussian random design model, i.e. the elements of measurement matrix are drawn from Gaussian distribution, is studied by literature. However, we find that these approaches are not suitable for row-orthogonal measurement matrices, which are of more practical relevance. In view of statistical mechanics approaches, we provide derivations of more accurate test statistics and thresholds (or p-values) under the row-orthogonal design model, and theoretically analyze the detection performance of the present detector. Such detector can analytically provide the threshold according to given false alarm rate, which is not possible with the conventional CS detector, and the detection performance is proved to be better than that of the traditional LASSO detector. Comparing with other debiased LASSO based detectors, simulation results indicate that the proposed approach can achieve more accurate probability of false alarm when the measurement matrix is row-orthogonal, leading to better detection performance under Neyman-Pearson principle.