Vincent Monardo
Theoretical Linear Convergence of Deep Unfolding Network for Block-Sparse Signal Recovery
Nov 18, 2021

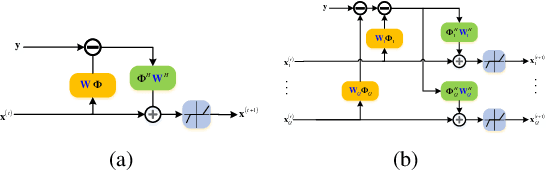
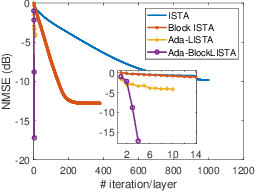
Abstract:In this paper, we consider the recovery of the high-dimensional block-sparse signal from a compressed set of measurements, where the non-zero coefficients of the recovered signal occur in a small number of blocks. Adopting the idea of deep unfolding, we explore the block-sparse structure and put forward a block-sparse reconstruction network named Ada-BlockLISTA, which performs gradient descent on every single block followed by a block-wise shrinkage. Furthermore, we prove the linear convergence rate of our proposed network, which also theoretically guarantees exact recovery for a potentially higher sparsity level based on underlyingblock structure. Numerical results indicate that Ada-BlockLISTA yields better signal recovery performance compared with existing algorithms, which ignore the additional block structure in the signal model.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge