Replicated Vector Approximate Message Passing For Resampling Problem
Paper and Code
May 23, 2019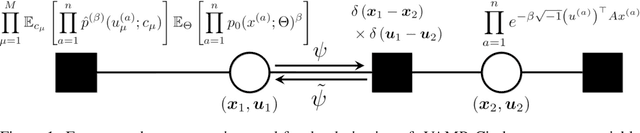
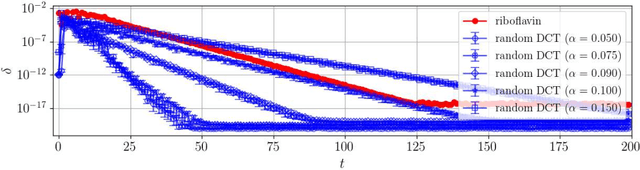
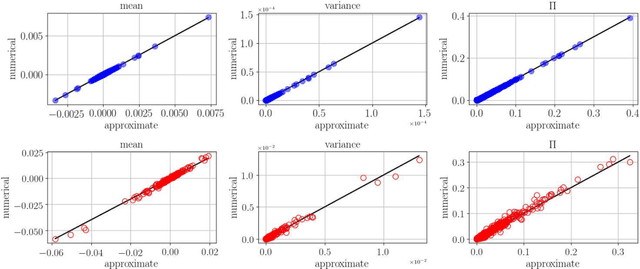
Resampling techniques are widely used in statistical inference and ensemble learning, in which estimators' statistical properties are essential. However, existing methods are computationally demanding, because repetitions of estimation/learning via numerical optimization/integral for each resampled data are required. In this study, we introduce a computationally efficient method to resolve such problem: replicated vector approximate message passing. This is based on a combination of the replica method of statistical physics and an accurate approximate inference algorithm, namely the vector approximate message passing of information theory. The method provides tractable densities without repeating estimation/learning, and the densities approximately offer an arbitrary degree of the estimators' moment in practical time. In the experiment, we apply the proposed method to the stability selection method, which is commonly used in variable selection problems. The numerical results show its fast convergence and high approximation accuracy for problems involving both synthetic and real-world datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge