Perfect reconstruction of sparse signals using nonconvexity control and one-step RSB message passing

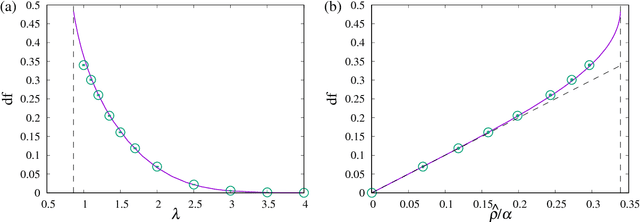
We consider sparse signal reconstruction via minimization of the smoothly clipped absolute deviation (SCAD) penalty, and develop one-step replica-symmetry-breaking (1RSB) extensions of approximate message passing (AMP), termed 1RSB-AMP. Starting from the 1RSB formulation of belief propagation, we derive explicit update rules of 1RSB-AMP together with the corresponding state evolution (1RSB-SE) equations. A detailed comparison shows that 1RSB-AMP and 1RSB-SE agree remarkably well at the macroscopic level, even in parameter regions where replica-symmetric (RS) AMP, termed RS-AMP, diverges and where the 1RSB description itself is not expected to be thermodynamically exact. Fixed-point analysis of 1RSB-SE reveals a phase diagram consisting of success, failure, and diverging phases, as in the RS case. However, the diverging-region boundary now depends on the Parisi parameter due to the 1RSB ansatz, and we propose a new criterion -- minimizing the size of the diverging region -- rather than the conventional zero-complexity condition, to determine its value. Combining this criterion with the nonconvexity-control (NCC) protocol proposed in a previous RS study improves the algorithmic limit of perfect reconstruction compared with RS-AMP. Numerical solutions of 1RSB-SE and experiments with 1RSB-AMP confirm that this improved limit is achieved in practice, though the gain is modest and remains slightly inferior to the Bayes-optimal threshold. We also report the behavior of thermodynamic quantities -- overlaps, free entropy, complexity, and the non-self-averaging susceptibility -- that characterize the 1RSB phase in this problem.

The Effect of Optimal Self-Distillation in Noisy Gaussian Mixture Model

Self-distillation (SD), a technique where a model refines itself from its own predictions, has garnered attention as a simple yet powerful approach in machine learning. Despite its widespread use, the mechanisms underlying its effectiveness remain unclear. In this study, we investigate the efficacy of hyperparameter-tuned multi-stage SD in binary classification tasks with noisy labeled Gaussian mixture data, utilizing a replica theory. Our findings reveals that the primary driver of SD's performance improvement is denoising through hard pseudo-labels, with the most notable gains observed in moderately sized datasets. We also demonstrate the efficacy of practical heuristics, such as early stopping for extracting meaningful signal and bias fixation for imbalanced data. These results provide both theoretical guarantees and practical insights, advancing our understanding and application of SD in noisy settings.

Effect of Weight Quantization on Learning Models by Typical Case Analysis

This paper examines the quantization methods used in large-scale data analysis models and their hyperparameter choices. The recent surge in data analysis scale has significantly increased computational resource requirements. To address this, quantizing model weights has become a prevalent practice in data analysis applications such as deep learning. Quantization is particularly vital for deploying large models on devices with limited computational resources. However, the selection of quantization hyperparameters, like the number of bits and value range for weight quantization, remains an underexplored area. In this study, we employ the typical case analysis from statistical physics, specifically the replica method, to explore the impact of hyperparameters on the quantization of simple learning models. Our analysis yields three key findings: (i) an unstable hyperparameter phase, known as replica symmetry breaking, occurs with a small number of bits and a large quantization width; (ii) there is an optimal quantization width that minimizes error; and (iii) quantization delays the onset of overparameterization, helping to mitigate overfitting as indicated by the double descent phenomenon. We also discover that non-uniform quantization can enhance stability. Additionally, we develop an approximate message-passing algorithm to validate our theoretical results.

Prediction Errors for Penalized Regressions based on Generalized Approximate Message Passing

We discuss the prediction accuracy of assumed statistical models in terms of prediction errors for the generalized linear model and penalized maximum likelihood methods. We derive the forms of estimators for the prediction errors: $C_p$ criterion, information criteria, and leave-one-out cross validation (LOOCV) error, using the generalized approximate message passing (GAMP) algorithm and replica method. These estimators coincide with each other when the number of model parameters is sufficiently small; however, there is a discrepancy between them in particular in the overparametrized region where the number of model parameters is larger than the data dimension. In this paper, we review the prediction errors and corresponding estimators, and discuss their differences. In the framework of GAMP, we show that the information criteria can be expressed by using the variance of the estimates. Further, we demonstrate how to approach LOOCV error from the information criteria by utilizing the expression provided by GAMP.

Active pooling design in group testing based on Bayesian posterior prediction

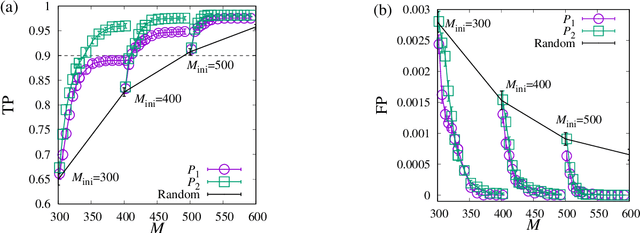
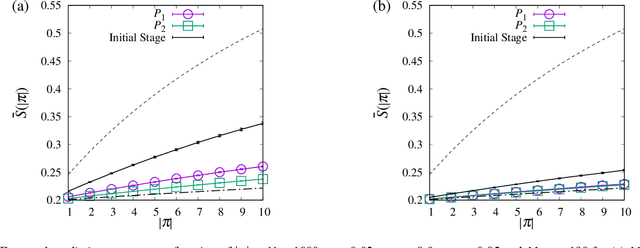
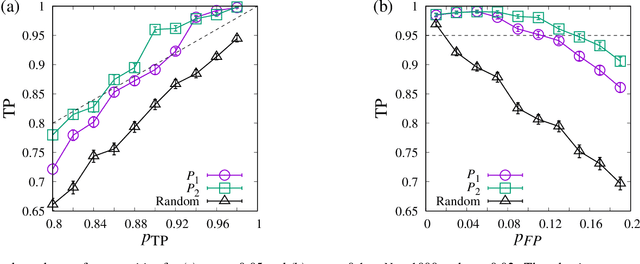
In identifying infected patients in a population, group testing is an effective method to reduce the number of tests and correct the test errors. In the group testing procedure, tests are performed on pools of specimens collected from patients, where the number of pools is lower than that of patients. The performance of group testing heavily depends on the design of pools and algorithms that are used in inferring the infected patients from the test outcomes. In this paper, an adaptive design method of pools based on the predictive distribution is proposed in the framework of Bayesian inference. The proposed method executed using the belief propagation algorithm results in more accurate identification of the infected patients, as compared to the group testing performed on random pools determined in advance.

Bayesian inference of infected patients in group testing with prevalence estimation

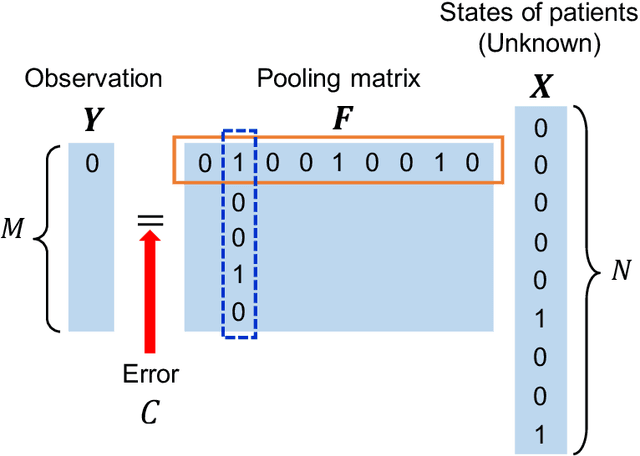
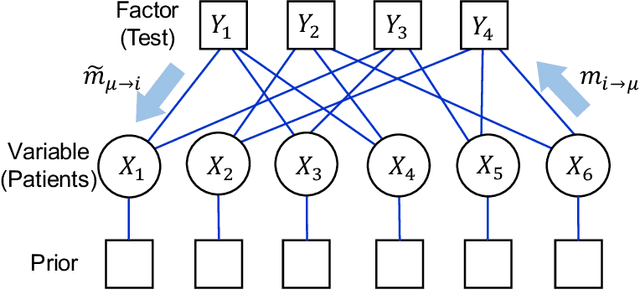
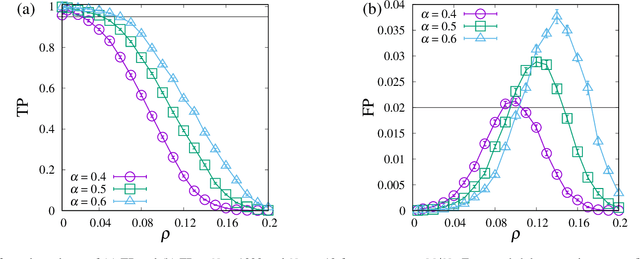
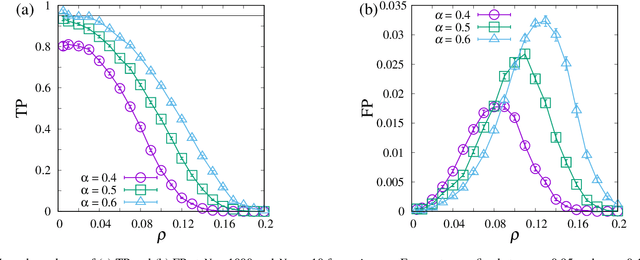
Group testing is a method of identifying infected patients by performing tests on a pool of specimens collected from patients. For the case in which the test returns a false result with finite probability, we propose Bayesian inference and a corresponding belief propagation (BP) algorithm to identify the infected patients from the results of tests performed on the pool. We show that the true-positive rate is improved by taking into account the credible interval of a point estimate of each patient. Further, the prevalence and the error probability in the test are estimated by combining an expectation-maximization method with the BP algorithm. As another approach, we introduce a hierarchical Bayes model to identify the infected patients and estimate the prevalence. By comparing these methods, we formulate a guide for practical usage.

Cross validation in sparse linear regression with piecewise continuous nonconvex penalties and its acceleration

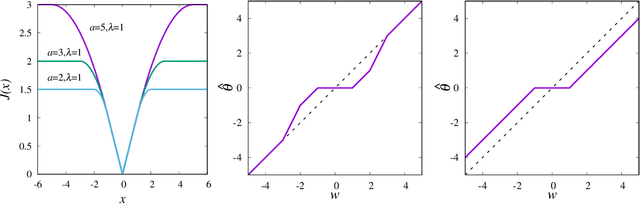
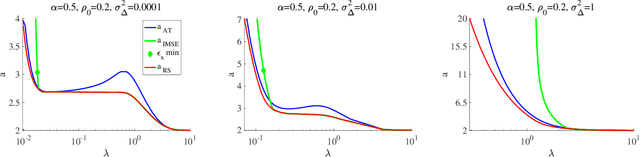
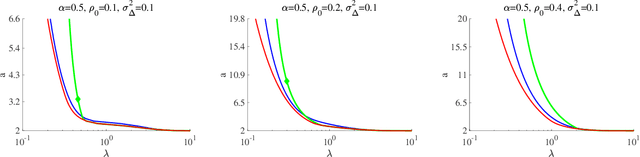
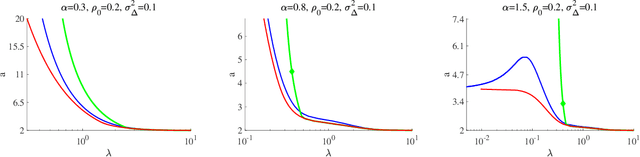
We investigate the signal reconstruction performance of sparse linear regression in the presence of noise when piecewise continuous nonconvex penalties are used. Among such penalties, we focus on the smoothly clipped absolute deviation (SCAD) penalty. The contributions of this study are three-fold: We first present a theoretical analysis of a typical reconstruction performance, using the replica method, under the assumption that each component of the design matrix is given as an independent and identically distributed (i.i.d.) Gaussian variable. This clarifies the superiority of the SCAD estimator compared with $\ell_1$ in a wide parameter range, although the nonconvex nature of the penalty tends to lead to solution multiplicity in certain regions. This multiplicity is shown to be connected to replica symmetry breaking in the spin-glass theory, and associated phase diagrams are given. We also show that the global minimum of the mean square error between the estimator and the true signal is located in the replica symmetric phase. Second, we develop an approximate formula efficiently computing the cross-validation error without actually conducting the cross-validation, which is also applicable to the non-i.i.d. design matrices. It is shown that this formula is only applicable to the unique solution region and tends to be unstable in the multiple solution region. We implement instability detection procedures, which allows the approximate formula to stand alone and resultantly enables us to draw phase diagrams for any specific dataset. Third, we propose an annealing procedure, called nonconvexity annealing, to obtain the solution path efficiently. Numerical simulations are conducted on simulated datasets to examine these results to verify the consistency of the theoretical results and the efficiency of the approximate formula and nonconvexity annealing.

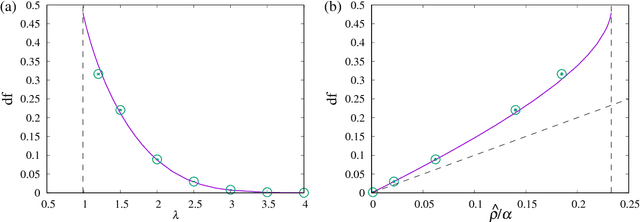
Perfect reconstruction of sparse signals with piecewise continuous nonconvex penalties and nonconvexity control

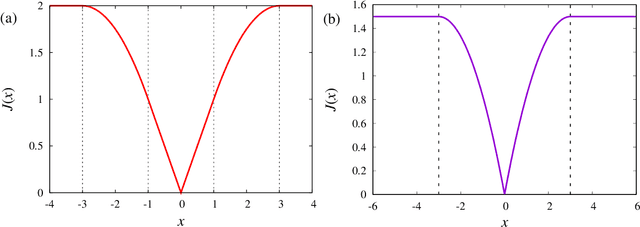
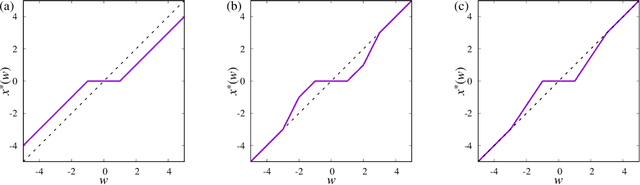
We consider compressed sensing formulated as a minimization problem of nonconvex sparse penalties, Smoothly Clipped Absolute deviation (SCAD) and Minimax Concave Penalty (MCP). The nonconvexity of these penalties is controlled by nonconvexity parameters, and L1 penalty is contained as a limit with respect to these parameters. The analytically derived reconstruction limit overcomes that of L1 and the algorithmic limit in the Bayes-optimal setting, when the nonconvexity parameters have suitable values. For the practical usage, we apply the approximate message passing (AMP) to these nonconvex penalties. We show that the performance of AMP is considerably improved by controlling nonconvexity parameters.

Estimator of Prediction Error Based on Approximate Message Passing for Penalized Linear Regression

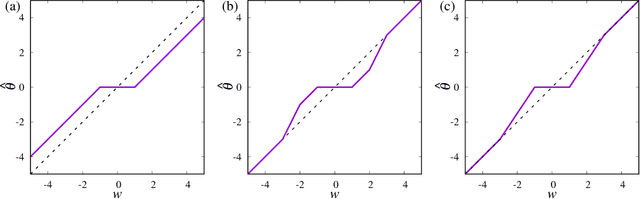
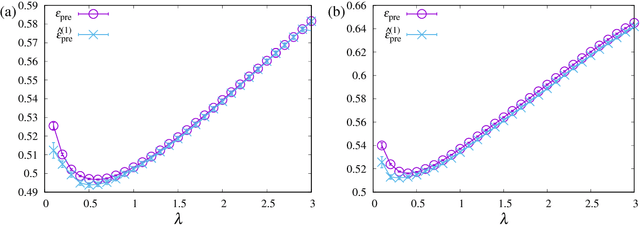
We propose an estimator of prediction error using an approximate message passing (AMP) algorithm that can be applied to a broad range of sparse penalties. Following Stein's lemma, the estimator of the generalized degrees of freedom, which is a key quantity for the construction of the estimator of the prediction error, is calculated at the AMP fixed point. The resulting form of the AMP-based estimator does not depend on the penalty function, and its value can be further improved by considering the correlation between predictors. The proposed estimator is asymptotically unbiased when the components of the predictors and response variables are independently generated according to a Gaussian distribution. We examine the behaviour of the estimator for real data under nonconvex sparse penalties, where Akaike's information criterion does not correspond to an unbiased estimator of the prediction error. The model selected by the proposed estimator is close to that which minimizes the true prediction error.

Approximate message passing for nonconvex sparse regularization with stability and asymptotic analysis

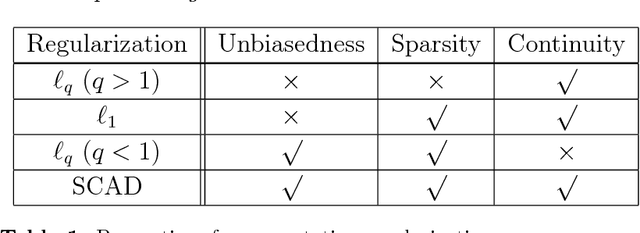
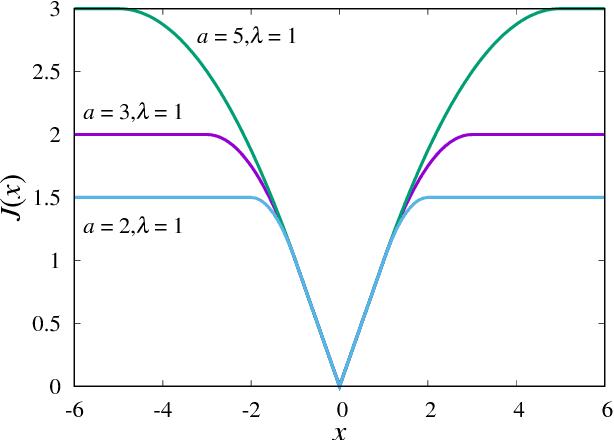
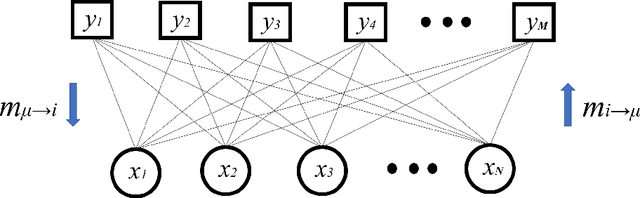
We analyse a linear regression problem with nonconvex regularization called smoothly clipped absolute deviation (SCAD) under an overcomplete Gaussian basis for Gaussian random data. We propose an approximate message passing (AMP) algorithm considering nonconvex regularization, namely SCAD-AMP, and analytically show that the stability condition corresponds to the de Almeida--Thouless condition in spin glass literature. Through asymptotic analysis, we show the correspondence between the density evolution of SCAD-AMP and the replica symmetric solution. Numerical experiments confirm that for a sufficiently large system size, SCAD-AMP achieves the optimal performance predicted by the replica method. Through replica analysis, a phase transition between replica symmetric (RS) and replica symmetry breaking (RSB) region is found in the parameter space of SCAD. The appearance of the RS region for a nonconvex penalty is a significant advantage that indicates the region of smooth landscape of the optimization problem. Furthermore, we analytically show that the statistical representation performance of the SCAD penalty is better than that of L1-based methods, and the minimum representation error under RS assumption is obtained at the edge of the RS/RSB phase. The correspondence between the convergence of the existing coordinate descent algorithm and RS/RSB transition is also indicated.