Perfect Reconstruction of Sparse Signals via Greedy Monte-Carlo Search
Paper and Code
Aug 24, 2020
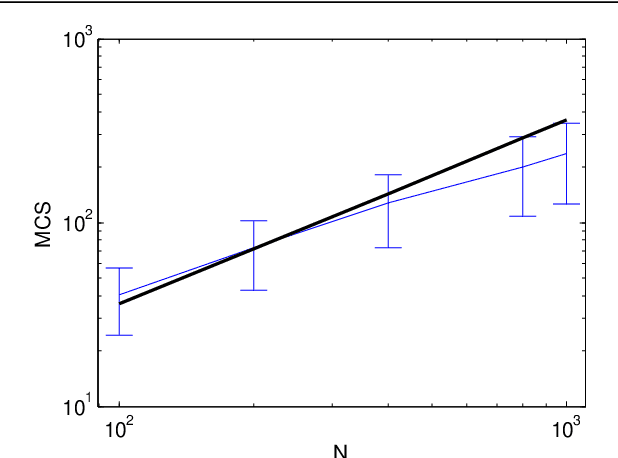


We propose a Monte-Carlo-based method for reconstructing sparse signals in the formulation of sparse linear regression in a high-dimensional setting. The basic idea of this algorithm is to explicitly select variables or covariates to represent a given data vector or responses and accept randomly generated updates of that selection if and only if the energy or cost function decreases. This algorithm is called the greedy Monte-Carlo (GMC) search algorithm. Its performance is examined via numerical experiments, which suggests that in the noiseless case, GMC can achieve perfect reconstruction in undersampling situations of a reasonable level: it can outperform the $\ell_1$ relaxation but does not reach the algorithmic limit of MC-based methods theoretically clarified by an earlier analysis. Additionally, an experiment on a real-world dataset supports the practicality of GMC.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge