$Ψ$-Bench: Evaluating Persona-Sensitive Influencing in Persuasive Dialogues

Personalization is a crucial capability of modern language agents. However, current research primarily positions personalized agents as passive responders to user preferences, limiting their ability to interact with users and provide suggestions or guidance proactively. To systematically evaluate such proactive personalization in realistic interactions, we propose $Ψ$-Bench, a benchmark for assessing LLMs' ability to influence realistic users through conversation. We design three real-world interaction scenarios that involve persuasion in $Ψ$-Bench, and endow simulated clients with personal characteristics through explicit user profiles derived from dialogue histories. We evaluate 10 frontier LLMs on $Ψ$-Bench and find that while most models can produce coherent and reasonable arguments, even state-of-the-art models still leave considerable room for improvement in persuasion. We also find that providing access to client profiles yields an average performance gain of 18.24\%, highlighting the importance of user-specific information for effective persuasion. Overall, our work highlights persona-sensitive influencing as a challenging yet practical direction for evaluating and developing more proactive personalized LLM agents. Codes are available at: https://github.com/Hanpx20/Psi-Bench.

Resolving Representation Ambiguity in Feedforward Novel View Synthesis Transformer via Semantic-Spatial Decoupling

Transformer-based models have advanced feedforward novel view synthesis (NVS). Current architectures such as GS-LRM and LVSM mix semantic information (e.g., RGB) and spatial information (e.g., Plücker rays) into a shared feature space. Since Plücker rays naturally carry lattice-like spatial structure, these designs can make the spatial bias interfere with appearance representation and degrade rendering fidelity. To this end, we propose to decouple the representation of feedforward NVS transformers into separate semantic and spatial tokens. The decoupled design keeps semantic and spatial information explicit in their branches while preserving cross-branch interaction through shared attention routing. Built on this design, we introduce optional categorized supervision and bidirectional modulation: the former provides branch-specific training signals, while the latter improves interaction between the two branches. Notably, the base decoupled design introduces virtually zero additional inference latency due to its architectural design. The proposed designs achieve consistent improvements, demonstrating effectiveness across decoder-only and encoder-decoder feedforward NVS models.

Useful Memories Become Faulty When Continuously Updated by LLMs

Learning from past experience benefits from two complementary forms of memory: episodic traces -- raw trajectories of what happened -- and consolidated abstractions distilled across many episodes into reusable, schema-like lessons. Recent agentic-memory systems pursue the consolidated form: an LLM rewrites past trajectories into a textual memory bank that it continuously updates with new interactions, promising self-improving agents without parameter updates. Yet we find that such consolidated memories produced by today's LLMs are often faulty even when derived from useful experiences. As consolidation proceeds, memory utility first rises, then degrades, and can fall below the no-memory baseline. More surprisingly, even when consolidating from ground-truth solutions, GPT-5.4 fails on 54% of a set of ARC-AGI problems it had previously solved without memory. We trace the regression to the consolidation step rather than the underlying experience: the same trajectories yield qualitatively different memories under different update schedules, and an episodic-only control that simply retains those trajectories remains competitive with the consolidators we test. In a controlled ARC-AGI Stream environment that exposes Retain, Delete, and Consolidate actions, agents preserve raw episodes by default and double the accuracy of their forced-consolidation counterparts; disabling consolidation entirely (episodic management only) matches this auto regime. Practically, robust agent memory should treat raw episodes as first-class evidence and gate consolidation explicitly rather than firing it after every interaction. Looking forward, reliable agentic memory will require LLMs that can consolidate without overwriting the evidence they depend on.

Classical and Quantum Speedups for Non-Convex Optimization via Energy Conserving Descent

The Energy Conserving Descent (ECD) algorithm was recently proposed (De Luca & Silverstein, 2022) as a global non-convex optimization method. Unlike gradient descent, appropriately configured ECD dynamics escape strict local minima and converge to a global minimum, making it appealing for machine learning optimization. We present the first analytical study of ECD, focusing on the one-dimensional setting for this first installment. We formalize a stochastic ECD dynamics (sECD) with energy-preserving noise, as well as a quantum analog of the ECD Hamiltonian (qECD), providing the foundation for a quantum algorithm through Hamiltonian simulation. For positive double-well objectives, we compute the expected hitting time from a local to the global minimum. We prove that both sECD and qECD yield exponential speedup over respective gradient descent baselines--stochastic gradient descent and its quantization. For objectives with tall barriers, qECD achieves a further speedup over sECD.

Efficient-LVSM: Faster, Cheaper, and Better Large View Synthesis Model via Decoupled Co-Refinement Attention

Feedforward models for novel view synthesis (NVS) have recently advanced by transformer-based methods like LVSM, using attention among all input and target views. In this work, we argue that its full self-attention design is suboptimal, suffering from quadratic complexity with respect to the number of input views and rigid parameter sharing among heterogeneous tokens. We propose Efficient-LVSM, a dual-stream architecture that avoids these issues with a decoupled co-refinement mechanism. It applies intra-view self-attention for input views and self-then-cross attention for target views, eliminating unnecessary computation. Efficient-LVSM achieves 29.86 dB PSNR on RealEstate10K with 2 input views, surpassing LVSM by 0.2 dB, with 2x faster training convergence and 4.4x faster inference speed. Efficient-LVSM achieves state-of-the-art performance on multiple benchmarks, exhibits strong zero-shot generalization to unseen view counts, and enables incremental inference with KV-cache, thanks to its decoupled designs.

Interleave-VLA: Enhancing Robot Manipulation with Interleaved Image-Text Instructions

Vision-Language-Action (VLA) models have shown great promise for generalist robotic manipulation in the physical world. However, existing models are restricted to robot observations and text-only instructions, lacking the flexibility of interleaved multimodal instructions enabled by recent advances in foundation models in the digital world. In this paper, we present Interleave-VLA, the first framework capable of comprehending interleaved image-text instructions and directly generating continuous action sequences in the physical world. It offers a flexible, model-agnostic paradigm that extends state-of-the-art VLA models with minimal modifications and strong zero-shot generalization. A key challenge in realizing Interleave-VLA is the absence of large-scale interleaved embodied datasets. To bridge this gap, we develop an automatic pipeline that converts text-only instructions from real-world datasets in Open X-Embodiment into interleaved image-text instructions, resulting in the first large-scale real-world interleaved embodied dataset with 210k episodes. Through comprehensive evaluation on simulation benchmarks and real-robot experiments, we demonstrate that Interleave-VLA offers significant benefits: 1) it improves out-of-domain generalization to unseen objects by 2-3x compared to state-of-the-art baselines, 2) supports flexible task interfaces, and 3) handles diverse user-provided image instructions in a zero-shot manner, such as hand-drawn sketches. We further analyze the factors behind Interleave-VLA's strong zero-shot performance, showing that the interleaved paradigm effectively leverages heterogeneous datasets and diverse instruction images, including those from the Internet, which demonstrates strong potential for scaling up. Our model and dataset will be open-sourced.

GraphEval: A Lightweight Graph-Based LLM Framework for Idea Evaluation

The powerful capabilities of Large Language Models (LLMs) have led to their growing use in evaluating human-generated content, particularly in evaluating research ideas within academic settings. Existing solutions primarily rely on prompt-based LLM methods or fine-tuned lightweight language models for idea evaluation. However, these methods are often unstable and struggle to comprehend the complex semantic information embedded in the ideas, impeding their ability to perform high-quality evaluations. To address the above challenges, we propose GraphEval, a lightweight graph-based LLM framework for idea evaluation. Our insight is that a complex idea can be broken down into comprehensible viewpoint nodes using prompts from small LLMs. These viewpoint nodes can then be linked together through edges created from LLM-based relation extraction and/or BERT similarity scores. The created viewpoint-graph can be used to conveniently propagate scores across view-nodes to improve the robustness of the idea evaluations. In particular, we propose two lightweight graph-based methods for idea evaluation: (1) GraphEval-LP: a training-free label propagation algorithm that propagates evaluation scores from known view-nodes to unknown nodes; (2) GraphEval-GNN: a Graph Neural Networks (GNN) that is trained to predict the evaluation scores given the observed graph with minimal computation resources. Moreover, to overcome LLM's limitation in objectively assessing the novelty of ideas, we further propose a novelty detection model to GraphEval-GNN to enhance its capability in judging idea novelty. Experiments on two datasets show GraphEval improves F1 scores by at least 14% with low computation and API costs. Additionally, GraphEval can effectively detect plagiarized ideas.

On the number of modes of Gaussian kernel density estimators

We consider the Gaussian kernel density estimator with bandwidth $\beta^{-\frac12}$ of $n$ iid Gaussian samples. Using the Kac-Rice formula and an Edgeworth expansion, we prove that the expected number of modes on the real line scales as $\Theta(\sqrt{\beta\log\beta})$ as $\beta,n\to\infty$ provided $n^c\lesssim \beta\lesssim n^{2-c}$ for some constant $c>0$. An impetus behind this investigation is to determine the number of clusters to which Transformers are drawn in a metastable state.

ProAgent: Building Proactive Cooperative AI with Large Language Models

Building AIs with adaptive behaviors in human-AI cooperation stands as a pivotal focus in AGI research. Current methods for developing cooperative agents predominantly rely on learning-based methods, where policy generalization heavily hinges on past interactions with specific teammates. These approaches constrain the agent's capacity to recalibrate its strategy when confronted with novel teammates. We propose \textbf{ProAgent}, a novel framework that harnesses large language models (LLMs) to fashion a \textit{pro}active \textit{agent} empowered with the ability to anticipate teammates' forthcoming decisions and formulate enhanced plans for itself. ProAgent excels at cooperative reasoning with the capacity to dynamically adapt its behavior to enhance collaborative efforts with teammates. Moreover, the ProAgent framework exhibits a high degree of modularity and interpretability, facilitating seamless integration to address a wide array of coordination scenarios. Experimental evaluations conducted within the framework of \textit{Overcook-AI} unveil the remarkable performance superiority of ProAgent, outperforming five methods based on self-play and population-based training in cooperation with AI agents. Further, when cooperating with human proxy models, its performance exhibits an average improvement exceeding 10\% compared to the current state-of-the-art, COLE. The advancement was consistently observed across diverse scenarios involving interactions with both AI agents of varying characteristics and human counterparts. These findings inspire future research for human-robot collaborations. For a hands-on demonstration, please visit \url{https://pku-proagent.github.io}.

Randomly Initialized One-Layer Neural Networks Make Data Linearly Separable

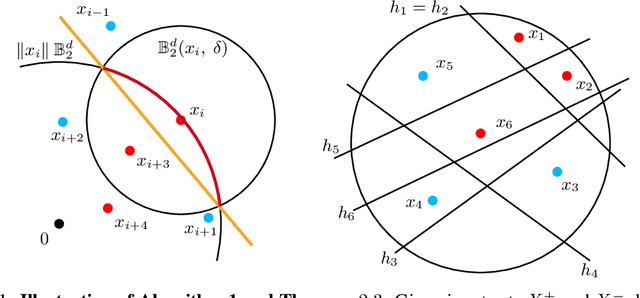
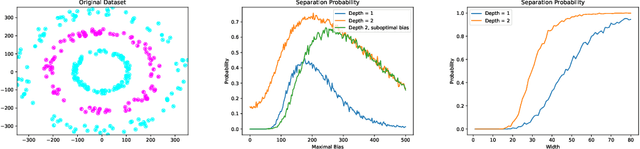
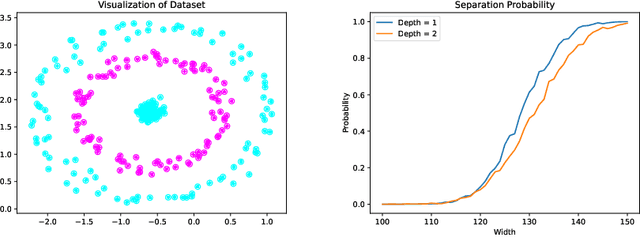
Recently, neural networks have been shown to perform exceptionally well in transforming two arbitrary sets into two linearly separable sets. Doing this with a randomly initialized neural network is of immense interest because the associated computation is cheaper than using fully trained networks. In this paper, we show that, with sufficient width, a randomly initialized one-layer neural network transforms two sets into two linearly separable sets with high probability. Furthermore, we provide explicit bounds on the required width of the neural network for this to occur. Our first bound is exponential in the input dimension and polynomial in all other parameters, while our second bound is independent of the input dimension, thereby overcoming the curse of dimensionality. We also perform an experimental study comparing the separation capacity of randomly initialized one-layer and two-layer neural networks. With correctly chosen biases, our study shows for low-dimensional data, the two-layer neural network outperforms the one-layer network. However, the opposite is observed for higher-dimensional data.