Random Latent Exploration for Deep Reinforcement Learning

The ability to efficiently explore high-dimensional state spaces is essential for the practical success of deep Reinforcement Learning (RL). This paper introduces a new exploration technique called Random Latent Exploration (RLE), that combines the strengths of bonus-based and noise-based (two popular approaches for effective exploration in deep RL) exploration strategies. RLE leverages the idea of perturbing rewards by adding structured random rewards to the original task rewards in certain (random) states of the environment, to encourage the agent to explore the environment during training. RLE is straightforward to implement and performs well in practice. To demonstrate the practical effectiveness of RLE, we evaluate it on the challenging Atari and IsaacGym benchmarks and show that RLE exhibits higher overall scores across all the tasks than other approaches.

Randomly Initialized One-Layer Neural Networks Make Data Linearly Separable

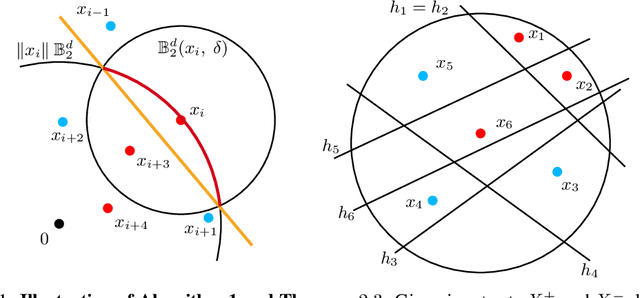
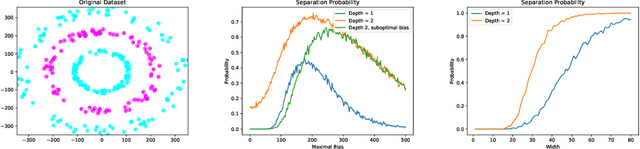
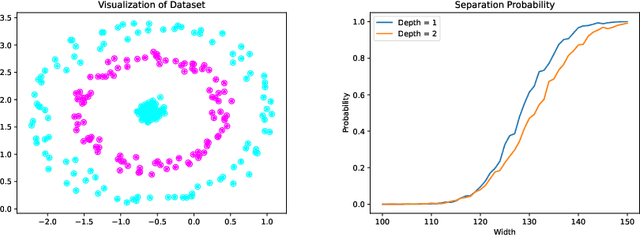
Recently, neural networks have been shown to perform exceptionally well in transforming two arbitrary sets into two linearly separable sets. Doing this with a randomly initialized neural network is of immense interest because the associated computation is cheaper than using fully trained networks. In this paper, we show that, with sufficient width, a randomly initialized one-layer neural network transforms two sets into two linearly separable sets with high probability. Furthermore, we provide explicit bounds on the required width of the neural network for this to occur. Our first bound is exponential in the input dimension and polynomial in all other parameters, while our second bound is independent of the input dimension, thereby overcoming the curse of dimensionality. We also perform an experimental study comparing the separation capacity of randomly initialized one-layer and two-layer neural networks. With correctly chosen biases, our study shows for low-dimensional data, the two-layer neural network outperforms the one-layer network. However, the opposite is observed for higher-dimensional data.