Xinshang Wang
Solver-in-the-Loop: MDP-Based Benchmarks for Self-Correction and Behavioral Rationality in Operations Research
Jan 28, 2026Abstract:Operations Research practitioners routinely debug infeasible models through an iterative process: analyzing Irreducible Infeasible Subsystems (\IIS{}), identifying constraint conflicts, and systematically repairing formulations until feasibility is achieved. Yet existing LLM benchmarks evaluate OR as one-shot translation -- given a problem description, generate solver code -- ignoring this diagnostic loop entirely. We introduce two benchmarks that place the \textbf{solver in the evaluation loop}. \textbf{\ORDebug{}} evaluates iterative self-correction through 5,000+ problems spanning 9 error types; each repair action triggers solver re-execution and \IIS{} recomputation, providing deterministic, verifiable feedback. \textbf{\ORBias{}} evaluates behavioral rationality through 2,000 newsvendor instances (1,000 ID + 1,000 OOD), measuring systematic deviations from closed-form optimal policies. Across 26 models and 12,000+ samples, we find that domain-specific RLVR training enables an 8B model to surpass frontier APIs: 95.3\% vs 86.2\% recovery rate (+9.1\%), 62.4\% vs 47.8\% diagnostic accuracy (+14.6\%), and 2.25 vs 3.78 steps to resolution (1.7$\times$ faster). On \ORBias{}, curriculum training achieves the only negative ID$\rightarrow$OOD bias drift among models evaluated (-9.6\%), reducing systematic bias by 48\% (from 20.0\% to 10.4\%). These results demonstrate that process-level evaluation with verifiable oracles enables targeted training that outperforms scale.
Optimizing LLM Inference: Fluid-Guided Online Scheduling with Memory Constraints
Apr 15, 2025



Abstract:Large Language Models (LLMs) are indispensable in today's applications, but their inference procedure -- generating responses by processing text in segments and using a memory-heavy Key-Value (KV) cache -- demands significant computational resources, particularly under memory constraints. This paper formulates LLM inference optimization as a multi-stage online scheduling problem where sequential prompt arrivals and KV cache growth render conventional scheduling ineffective. We develop a fluid dynamics approximation to provide a tractable benchmark that guides algorithm design. Building on this, we propose the Waiting for Accumulated Inference Threshold (WAIT) algorithm, which uses multiple thresholds to schedule incoming prompts optimally when output lengths are known, and extend it to Nested WAIT for cases with unknown output lengths. Theoretical analysis shows that both algorithms achieve near-optimal performance against the fluid benchmark in heavy traffic conditions, balancing throughput, latency, and Time to First Token (TTFT). Experiments with the Llama-7B model on an A100 GPU using both synthetic and real-world datasets demonstrate improved throughput and reduced latency relative to established baselines like vLLM and Sarathi. This work bridges operations research and machine learning, offering a rigorous framework for the efficient deployment of LLMs under memory constraints.
DOCS: Quantifying Weight Similarity for Deeper Insights into Large Language Models
Jan 28, 2025
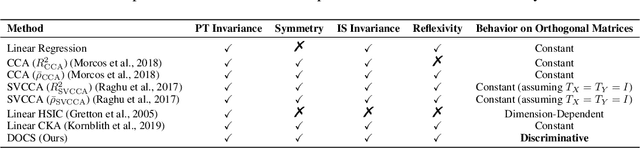

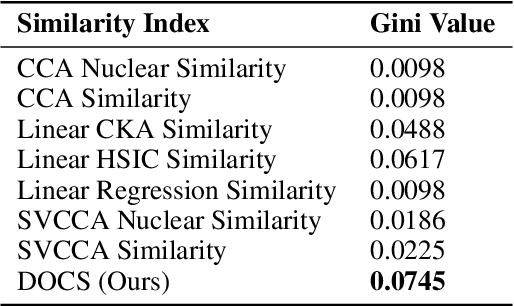
Abstract:We introduce a novel index, the Distribution of Cosine Similarity (DOCS), for quantitatively assessing the similarity between weight matrices in Large Language Models (LLMs), aiming to facilitate the analysis of their complex architectures. Leveraging DOCS, our analysis uncovers intriguing patterns in the latest open-source LLMs: adjacent layers frequently exhibit high weight similarity and tend to form clusters, suggesting depth-wise functional specialization. Additionally, we prove that DOCS is theoretically effective in quantifying similarity for orthogonal matrices, a crucial aspect given the prevalence of orthogonal initializations in LLMs. This research contributes to a deeper understanding of LLM architecture and behavior, offering tools with potential implications for developing more efficient and interpretable models.
Expressive Power of Graph Neural Networks for Quadratic Programs
Jun 09, 2024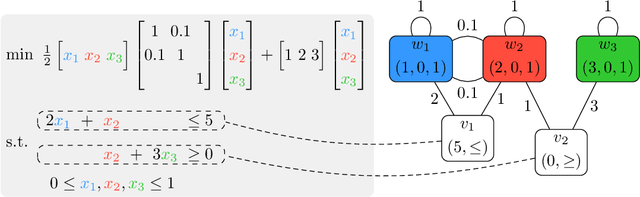
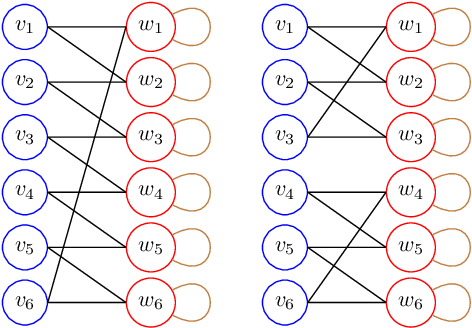
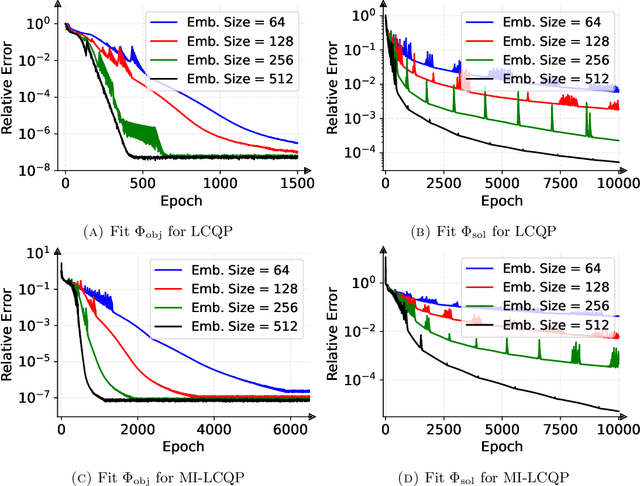
Abstract:Quadratic programming (QP) is the most widely applied category of problems in nonlinear programming. Many applications require real-time/fast solutions, though not necessarily with high precision. Existing methods either involve matrix decomposition or use the preconditioned conjugate gradient method. For relatively large instances, these methods cannot achieve the real-time requirement unless there is an effective precondition. Recently, graph neural networks (GNNs) opened new possibilities for QP. Some promising empirical studies of applying GNNs for QP tasks show that GNNs can capture key characteristics of an optimization instance and provide adaptive guidance accordingly to crucial configurations during the solving process, or directly provide an approximate solution. Despite notable empirical observations, theoretical foundations are still lacking. In this work, we investigate the expressive or representative power of GNNs, a crucial aspect of neural network theory, specifically in the context of QP tasks, with both continuous and mixed-integer settings. We prove the existence of message-passing GNNs that can reliably represent key properties of quadratic programs, including feasibility, optimal objective value, and optimal solution. Our theory is validated by numerical results.
Rethinking the Capacity of Graph Neural Networks for Branching Strategy
Feb 11, 2024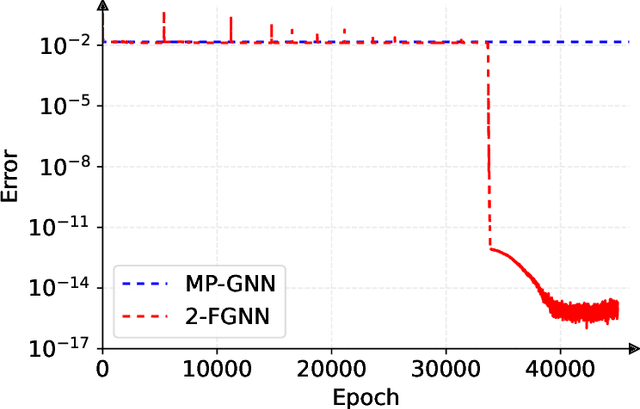
Abstract:Graph neural networks (GNNs) have been widely used to predict properties and heuristics of mixed-integer linear programs (MILPs) and hence accelerate MILP solvers. This paper investigates the capacity of GNNs to represent strong branching (SB) scores that provide an efficient strategy in the branch-and-bound algorithm. Although message-passing GNN (MP-GNN), as the simplest GNN structure, is frequently employed in the existing literature to learn SB scores, we prove a fundamental limitation in its expressive power -- there exist two MILP instances with different SB scores that cannot be distinguished by any MP-GNN, regardless of the number of parameters. In addition, we establish a universal approximation theorem for another GNN structure called the second-order folklore GNN (2-FGNN). We show that for any data distribution over MILPs, there always exists a 2-FGNN that can approximate the SB score with arbitrarily high accuracy and arbitrarily high probability. A small-scale numerical experiment is conducted to directly validate our theoretical findings.
DIG-MILP: a Deep Instance Generator for Mixed-Integer Linear Programming with Feasibility Guarantee
Oct 20, 2023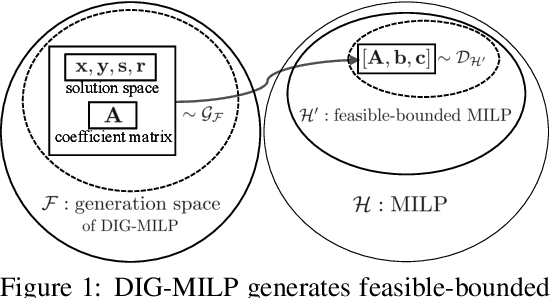

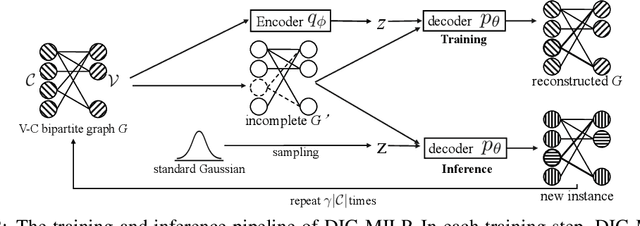

Abstract:Mixed-integer linear programming (MILP) stands as a notable NP-hard problem pivotal to numerous crucial industrial applications. The development of effective algorithms, the tuning of solvers, and the training of machine learning models for MILP resolution all hinge on access to extensive, diverse, and representative data. Yet compared to the abundant naturally occurring data in image and text realms, MILP is markedly data deficient, underscoring the vital role of synthetic MILP generation. We present DIG-MILP, a deep generative framework based on variational auto-encoder (VAE), adept at extracting deep-level structural features from highly limited MILP data and producing instances that closely mirror the target data. Notably, by leveraging the MILP duality, DIG-MILP guarantees a correct and complete generation space as well as ensures the boundedness and feasibility of the generated instances. Our empirical study highlights the novelty and quality of the instances generated by DIG-MILP through two distinct downstream tasks: (S1) Data sharing, where solver solution times correlate highly positive between original and DIG-MILP-generated instances, allowing data sharing for solver tuning without publishing the original data; (S2) Data Augmentation, wherein the DIG-MILP-generated instances bolster the generalization performance of machine learning models tasked with resolving MILP problems.
On Representing Mixed-Integer Linear Programs by Graph Neural Networks
Oct 19, 2022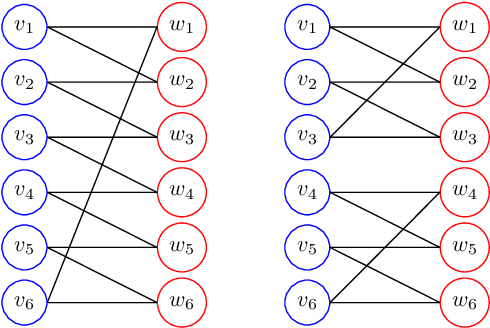
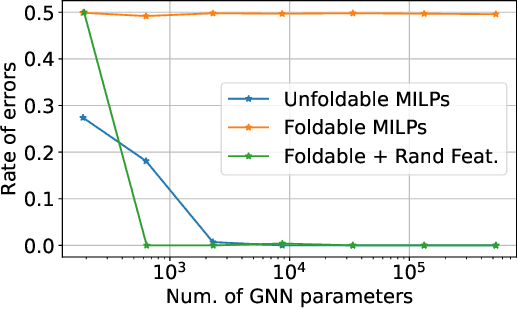
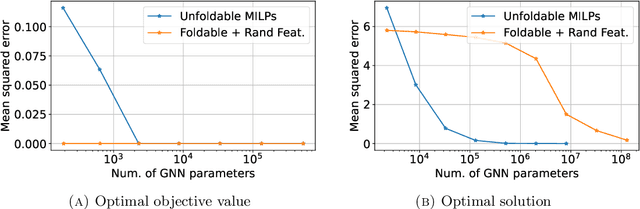
Abstract:While Mixed-integer linear programming (MILP) is NP-hard in general, practical MILP has received roughly 100--fold speedup in the past twenty years. Still, many classes of MILPs quickly become unsolvable as their sizes increase, motivating researchers to seek new acceleration techniques for MILPs. With deep learning, they have obtained strong empirical results, and many results were obtained by applying graph neural networks (GNNs) to making decisions in various stages of MILP solution processes. This work discovers a fundamental limitation: there exist feasible and infeasible MILPs that all GNNs will, however, treat equally, indicating GNN's lacking power to express general MILPs. Then, we show that, by restricting the MILPs to unfoldable ones or by adding random features, there exist GNNs that can reliably predict MILP feasibility, optimal objective values, and optimal solutions up to prescribed precision. We conducted small-scale numerical experiments to validate our theoretical findings.
On Representing Linear Programs by Graph Neural Networks
Sep 25, 2022

Abstract:Learning to optimize is a rapidly growing area that aims to solve optimization problems or improve existing optimization algorithms using machine learning (ML). In particular, the graph neural network (GNN) is considered a suitable ML model for optimization problems whose variables and constraints are permutation--invariant, for example, the linear program (LP). While the literature has reported encouraging numerical results, this paper establishes the theoretical foundation of applying GNNs to solving LPs. Given any size limit of LPs, we construct a GNN that maps different LPs to different outputs. We show that properly built GNNs can reliably predict feasibility, boundedness, and an optimal solution for each LP in a broad class. Our proofs are based upon the recently--discovered connections between the Weisfeiler--Lehman isomorphism test and the GNN. To validate our results, we train a simple GNN and present its accuracy in mapping LPs to their feasibilities and solutions.
Conservative Exploration for Semi-Bandits with Linear Generalization: A Product Selection Problem for Urban Warehouses
Mar 19, 2019



Abstract:The recent rising popularity of ultra-fast delivery services on retail platforms fuels the increasing use of urban warehouses, whose proximity to customers makes fast deliveries viable. The space limit in urban warehouses poses a problem for the online retailers: the number of products (SKUs) they carry is no longer "the more, the better", yet it can still be significantly large, reaching hundreds or thousands in a product category. In this paper, we study algorithms for dynamically identifying a large number of products (i.e., SKUs) with top customer purchase probabilities on the fly, from an ocean of potential products to offer on retailers' ultra-fast delivery platforms. We distill the product selection problem into a semi-bandit model with linear generalization. There are in total $N$ different arms, each with a feature vector of dimension $d$. The player pulls $K$ arms in each period and observes the bandit feedback from each of the pulled arms. We focus on the setting where $K$ is much greater than the number of total time periods $T$ or the dimension of product features $d$. We first analyze a standard UCB algorithm and show its regret bound can be expressed as the sum of a $T$-independent part $\tilde O(K d^{3/2})$ and a $T$-dependent part $\tilde O(d\sqrt{KT})$, which we refer to as "fixed cost" and "variable cost" respectively. To reduce the fixed cost for large $K$ values, we propose a novel online learning algorithm, with more conservative exploration steps, and show its fixed cost is reduced by a factor of $d$ to $\tilde O(K \sqrt{d})$. Moreover, we test the algorithms on an industrial dataset from Alibaba Group. Experimental results show that our new algorithm reduces the total regret of the standard UCB algorithm by at least 10%.
The Lingering of Gradients: How to Reuse Gradients over Time
Jan 09, 2019



Abstract:Classically, the time complexity of a first-order method is estimated by its number of gradient computations. In this paper, we study a more refined complexity by taking into account the "lingering" of gradients: once a gradient is computed at $x_k$, the additional time to compute gradients at $x_{k+1},x_{k+2},\dots$ may be reduced. We show how this improves the running time of gradient descent and SVRG. For instance, if the "additional time" scales linearly with respect to the traveled distance, then the "convergence rate" of gradient descent can be improved from $1/T$ to $\exp(-T^{1/3})$. On the empirical side, we solve a hypothetical revenue management problem on the Yahoo! Front Page Today Module application with 4.6m users to $10^{-6}$ error (or $10^{-12}$ dual error) using 6 passes of the dataset.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge