Prediction-Guided Active Experiments

In this work, we introduce a new framework for active experimentation, the Prediction-Guided Active Experiment (PGAE), which leverages predictions from an existing machine learning model to guide sampling and experimentation. Specifically, at each time step, an experimental unit is sampled according to a designated sampling distribution, and the actual outcome is observed based on an experimental probability. Otherwise, only a prediction for the outcome is available. We begin by analyzing the non-adaptive case, where full information on the joint distribution of the predictor and the actual outcome is assumed. For this scenario, we derive an optimal experimentation strategy by minimizing the semi-parametric efficiency bound for the class of regular estimators. We then introduce an estimator that meets this efficiency bound, achieving asymptotic optimality. Next, we move to the adaptive case, where the predictor is continuously updated with newly sampled data. We show that the adaptive version of the estimator remains efficient and attains the same semi-parametric bound under certain regularity assumptions. Finally, we validate PGAE's performance through simulations and a semi-synthetic experiment using data from the US Census Bureau. The results underscore the PGAE framework's effectiveness and superiority compared to other existing methods.

Online Local False Discovery Rate Control: A Resource Allocation Approach

We consider the problem of online local false discovery rate (FDR) control where multiple tests are conducted sequentially, with the goal of maximizing the total expected number of discoveries. We formulate the problem as an online resource allocation problem with accept/reject decisions, which from a high level can be viewed as an online knapsack problem, with the additional uncertainty of random budget replenishment. We start with general arrival distributions and propose a simple policy that achieves a $O(\sqrt{T})$ regret. We complement the result by showing that such regret rate is in general not improvable. We then shift our focus to discrete arrival distributions. We find that many existing re-solving heuristics in the online resource allocation literature, albeit achieve bounded loss in canonical settings, may incur a $\Omega(\sqrt{T})$ or even a $\Omega(T)$ regret. With the observation that canonical policies tend to be too optimistic and over accept arrivals, we propose a novel policy that incorporates budget buffers. We show that small additional logarithmic buffers suffice to reduce the regret from $\Omega(\sqrt{T})$ or even $\Omega(T)$ to $O(\ln^2 T)$. Numerical experiments are conducted to validate our theoretical findings. Our formulation may have wider applications beyond the problem considered in this paper, and our results emphasize how effective policies should be designed to reach a balance between circumventing wrong accept and reducing wrong reject in online resource allocation problems with uncertain budgets.

Asynchronous Gradient Play in Zero-Sum Multi-agent Games

Finding equilibria via gradient play in competitive multi-agent games has been attracting a growing amount of attention in recent years, with emphasis on designing efficient strategies where the agents operate in a decentralized and symmetric manner with guaranteed convergence. While significant efforts have been made in understanding zero-sum two-player matrix games, the performance in zero-sum multi-agent games remains inadequately explored, especially in the presence of delayed feedbacks, leaving the scalability and resiliency of gradient play open to questions. In this paper, we make progress by studying asynchronous gradient plays in zero-sum polymatrix games under delayed feedbacks. We first establish that the last iterate of entropy-regularized optimistic multiplicative weight updates (OMWU) method converges linearly to the quantal response equilibrium (QRE), the solution concept under bounded rationality, in the absence of delays. While the linear convergence continues to hold even when the feedbacks are randomly delayed under mild statistical assumptions, it converges at a noticeably slower rate due to a smaller tolerable range of learning rates. Moving beyond, we demonstrate entropy-regularized OMWU -- by adopting two-timescale learning rates in a delay-aware manner -- enjoys faster last-iterate convergence under fixed delays, and continues to converge provably even when the delays are arbitrarily bounded in an average-iterate manner. Our methods also lead to finite-time guarantees to approximate the Nash equilibrium (NE) by moderating the amount of regularization. To the best of our knowledge, this work is the first that aims to understand asynchronous gradient play in zero-sum polymatrix games under a wide range of delay assumptions, highlighting the role of learning rates separation.

Riemannian Natural Gradient Methods

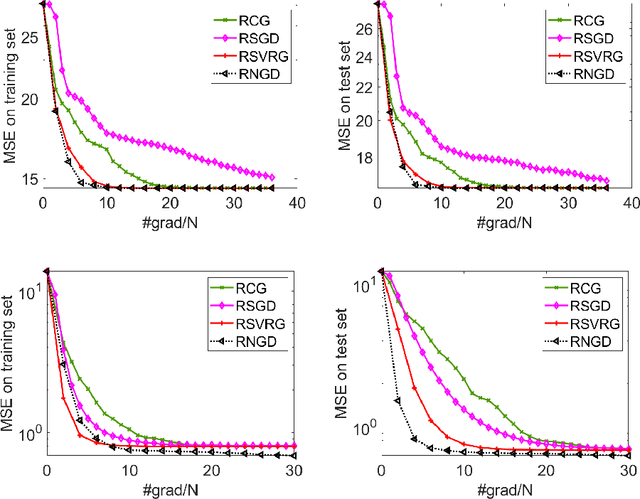
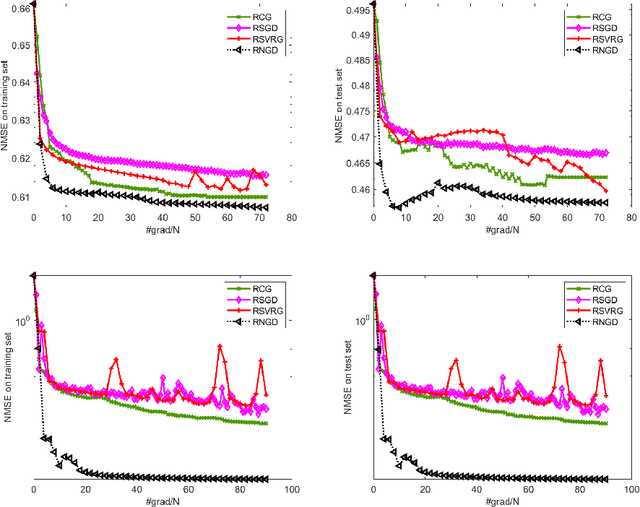
This paper studies large-scale optimization problems on Riemannian manifolds whose objective function is a finite sum of negative log-probability losses. Such problems arise in various machine learning and signal processing applications. By introducing the notion of Fisher information matrix in the manifold setting, we propose a novel Riemannian natural gradient method, which can be viewed as a natural extension of the natural gradient method from the Euclidean setting to the manifold setting. We establish the almost-sure global convergence of our proposed method under standard assumptions. Moreover, we show that if the loss function satisfies certain convexity and smoothness conditions and the input-output map satisfies a Riemannian Jacobian stability condition, then our proposed method enjoys a local linear -- or, under the Lipschitz continuity of the Riemannian Jacobian of the input-output map, even quadratic -- rate of convergence. We then prove that the Riemannian Jacobian stability condition will be satisfied by a two-layer fully connected neural network with batch normalization with high probability, provided that the width of the network is sufficiently large. This demonstrates the practical relevance of our convergence rate result. Numerical experiments on applications arising from machine learning demonstrate the advantages of the proposed method over state-of-the-art ones.