Non-Asymptotic Global Convergence of PPO-Clip

Reinforcement learning (RL) has gained attention for aligning large language models (LLMs) via reinforcement learning from human feedback (RLHF). The actor-only variants of Proximal Policy Optimization (PPO) are widely applied for their efficiency. These algorithms incorporate a clipping mechanism to improve stability. Besides, a regularization term, such as the reverse KL-divergence or a more general \(f\)-divergence, is introduced to prevent policy drift. Despite their empirical success, a rigorous theoretical understanding of the problem and the algorithm's properties is limited. This paper advances the theoretical foundations of the PPO-Clip algorithm by analyzing a deterministic actor-only PPO algorithm within the general RL setting with \(f\)-divergence regularization under the softmax policy parameterization. We derive a non-uniform Lipschitz smoothness condition and a Łojasiewicz inequality for the considered problem. Based on these, a non-asymptotic linear convergence rate to the globally optimal policy is established for the forward KL-regularizer. Furthermore, stationary convergence and local linear convergence are derived for the reverse KL-regularizer.

Translating Informal Proofs into Formal Proofs Using a Chain of States

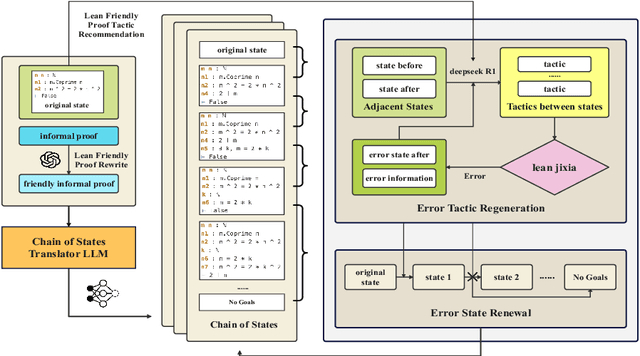
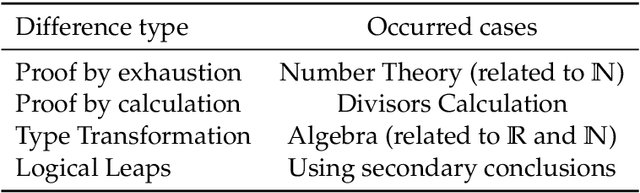
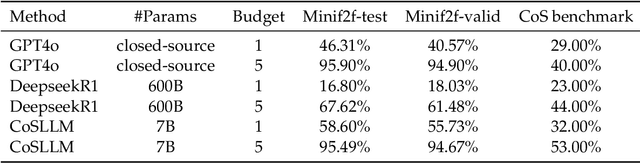
We address the problem of translating informal mathematical proofs expressed in natural language into formal proofs in Lean4 under a constrained computational budget. Our approach is grounded in two key insights. First, informal proofs tend to proceed via a sequence of logical transitions - often implications or equivalences - without explicitly specifying intermediate results or auxiliary lemmas. In contrast, formal systems like Lean require an explicit representation of each proof state and the tactics that connect them. Second, each informal reasoning step can be viewed as an abstract transformation between proof states, but identifying the corresponding formal tactics often requires nontrivial domain knowledge and precise control over proof context. To bridge this gap, we propose a two stage framework. Rather than generating formal tactics directly, we first extract a Chain of States (CoS), a sequence of intermediate formal proof states aligned with the logical structure of the informal argument. We then generate tactics to transition between adjacent states in the CoS, thereby constructing the full formal proof. This intermediate representation significantly reduces the complexity of tactic generation and improves alignment with informal reasoning patterns. We build dedicated datasets and benchmarks for training and evaluation, and introduce an interactive framework to support tactic generation from formal states. Empirical results show that our method substantially outperforms existing baselines, achieving higher proof success rates.

Advancing Mathematical Research via Human-AI Interactive Theorem Proving

We investigate how large language models can be used as research tools in scientific computing while preserving mathematical rigor. We propose a human-in-the-loop workflow for interactive theorem proving and discovery with LLMs. Human experts retain control over problem formulation and admissible assumptions, while the model searches for proofs or contradictions, proposes candidate properties and theorems, and helps construct structures and parameters that satisfy explicit constraints, supported by numerical experiments and simple verification checks. Experts treat these outputs as raw material, further refine them, and organize the results into precise statements and rigorous proofs. We instantiate this workflow in a case study on the connection between manifold optimization and Grover's quantum search algorithm, where the pipeline helps identify invariant subspaces, explore Grover-compatible retractions, and obtain convergence guarantees for the retraction-based gradient method. The framework provides a practical template for integrating large language models into frontier mathematical research, enabling faster exploration of proof space and algorithm design while maintaining transparent reasoning responsibilities. Although illustrated on manifold optimization problems in quantum computing, the principles extend to other core areas of scientific computing.

SITA: A Framework for Structure-to-Instance Theorem Autoformalization

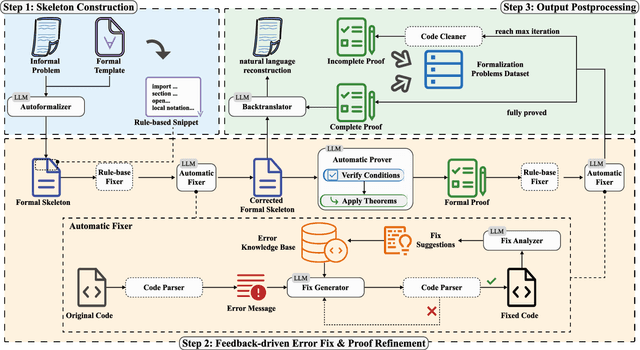
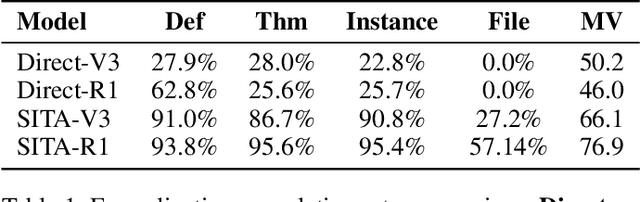
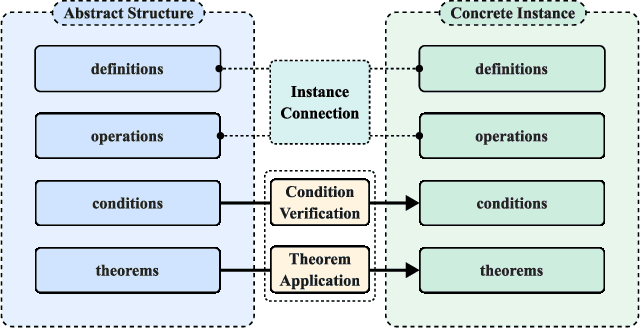
While large language models (LLMs) have shown progress in mathematical reasoning, they still face challenges in formalizing theorems that arise from instantiating abstract structures in concrete settings. With the goal of auto-formalizing mathematical results at the research level, we develop a framework for structure-to-instance theorem autoformalization (SITA), which systematically bridges the gap between abstract mathematical theories and their concrete applications in Lean proof assistant. Formalized abstract structures are treated as modular templates that contain definitions, assumptions, operations, and theorems. These templates serve as reusable guides for the formalization of concrete instances. Given a specific instantiation, we generate corresponding Lean definitions and instance declarations, integrate them using Lean's typeclass mechanism, and construct verified theorems by checking structural assumptions. We incorporate LLM-based generation with feedback-guided refinement to ensure both automation and formal correctness. Experiments on a dataset of optimization problems demonstrate that SITA effectively formalizes diverse instances grounded in abstract structures.

Accelerating Optimization via Differentiable Stopping Time

Optimization is an important module of modern machine learning applications. Tremendous efforts have been made to accelerate optimization algorithms. A common formulation is achieving a lower loss at a given time. This enables a differentiable framework with respect to the algorithm hyperparameters. In contrast, its dual, minimizing the time to reach a target loss, is believed to be non-differentiable, as the time is not differentiable. As a result, it usually serves as a conceptual framework or is optimized using zeroth-order methods. To address this limitation, we propose a differentiable stopping time and theoretically justify it based on differential equations. An efficient algorithm is designed to backpropagate through it. As a result, the proposed differentiable stopping time enables a new differentiable formulation for accelerating algorithms. We further discuss its applications, such as online hyperparameter tuning and learning to optimize. Our proposed methods show superior performance in comprehensive experiments across various problems, which confirms their effectiveness.

LMask: Learn to Solve Constrained Routing Problems with Lazy Masking

Routing problems are canonical combinatorial optimization tasks with wide-ranging applications in logistics, transportation, and supply chain management. However, solving these problems becomes significantly more challenging when complex constraints are involved. In this paper, we propose LMask, a novel learning framework that utilizes dynamic masking to generate high-quality feasible solutions for constrained routing problems. LMask introduces the LazyMask decoding method, which lazily refines feasibility masks with the backtracking mechanism. In addition, it employs the refinement intensity embedding to encode the search trace into the model, mitigating representation ambiguities induced by backtracking. To further reduce sampling cost, LMask sets a backtracking budget during decoding, while constraint violations are penalized in the loss function during training to counteract infeasibility caused by this budget. We provide theoretical guarantees for the validity and probabilistic optimality of our approach. Extensive experiments on the traveling salesman problem with time windows (TSPTW) and TSP with draft limits (TSPDL) demonstrate that LMask achieves state-of-the-art feasibility rates and solution quality, outperforming existing neural methods.

A Memory Efficient Randomized Subspace Optimization Method for Training Large Language Models

The memory challenges associated with training Large Language Models (LLMs) have become a critical concern, particularly when using the Adam optimizer. To address this issue, numerous memory-efficient techniques have been proposed, with GaLore standing out as a notable example designed to reduce the memory footprint of optimizer states. However, these approaches do not alleviate the memory burden imposed by activations, rendering them unsuitable for scenarios involving long context sequences or large mini-batches. Moreover, their convergence properties are still not well-understood in the literature. In this work, we introduce a Randomized Subspace Optimization framework for pre-training and fine-tuning LLMs. Our approach decomposes the high-dimensional training problem into a series of lower-dimensional subproblems. At each iteration, a random subspace is selected, and the parameters within that subspace are optimized. This structured reduction in dimensionality allows our method to simultaneously reduce memory usage for both activations and optimizer states. We establish comprehensive convergence guarantees and derive rates for various scenarios, accommodating different optimization strategies to solve the subproblems. Extensive experiments validate the superior memory and communication efficiency of our method, achieving performance comparable to GaLore and Adam.

Enhancing Zeroth-order Fine-tuning for Language Models with Low-rank Structures

Parameter-efficient fine-tuning (PEFT) significantly reduces memory costs when adapting large language models (LLMs) for downstream applications. However, traditional first-order (FO) fine-tuning algorithms incur substantial memory overhead due to the need to store activation values for back-propagation during gradient computation, particularly in long-context fine-tuning tasks. Zeroth-order (ZO) algorithms offer a promising alternative by approximating gradients using finite differences of function values, thus eliminating the need for activation storage. Nevertheless, existing ZO methods struggle to capture the low-rank gradient structure common in LLM fine-tuning, leading to suboptimal performance. This paper proposes a low-rank ZO gradient estimator and introduces a novel low-rank ZO algorithm (LOZO) that effectively captures this structure in LLMs. We provide convergence guarantees for LOZO by framing it as a subspace optimization method. Additionally, its low-rank nature enables LOZO to integrate with momentum techniques while incurring negligible extra memory costs. Extensive experiments across various model sizes and downstream tasks demonstrate that LOZO and its momentum-based variant outperform existing ZO methods and closely approach the performance of FO algorithms.

ODE-based Learning to Optimize

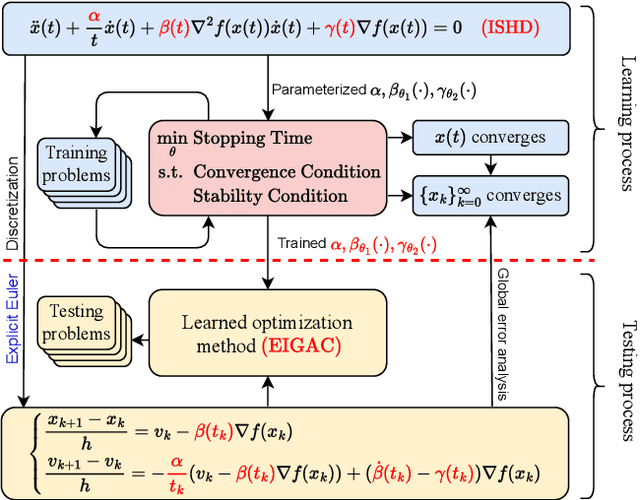
Recent years have seen a growing interest in understanding acceleration methods through the lens of ordinary differential equations (ODEs). Despite the theoretical advancements, translating the rapid convergence observed in continuous-time models to discrete-time iterative methods poses significant challenges. In this paper, we present a comprehensive framework integrating the inertial systems with Hessian-driven damping equation (ISHD) and learning-based approaches for developing optimization methods through a deep synergy of theoretical insights. We first establish the convergence condition for ensuring the convergence of the solution trajectory of ISHD. Then, we show that provided the stability condition, another relaxed requirement on the coefficients of ISHD, the sequence generated through the explicit Euler discretization of ISHD converges, which gives a large family of practical optimization methods. In order to select the best optimization method in this family for certain problems, we introduce the stopping time, the time required for an optimization method derived from ISHD to achieve a predefined level of suboptimality. Then, we formulate a novel learning to optimize (L2O) problem aimed at minimizing the stopping time subject to the convergence and stability condition. To navigate this learning problem, we present an algorithm combining stochastic optimization and the penalty method (StoPM). The convergence of StoPM using the conservative gradient is proved. Empirical validation of our framework is conducted through extensive numerical experiments across a diverse set of optimization problems. These experiments showcase the superior performance of the learned optimization methods.

An Improved Finite-time Analysis of Temporal Difference Learning with Deep Neural Networks

Temporal difference (TD) learning algorithms with neural network function parameterization have well-established empirical success in many practical large-scale reinforcement learning tasks. However, theoretical understanding of these algorithms remains challenging due to the nonlinearity of the action-value approximation. In this paper, we develop an improved non-asymptotic analysis of the neural TD method with a general $L$-layer neural network. New proof techniques are developed and an improved new $\tilde{\mathcal{O}}(\epsilon^{-1})$ sample complexity is derived. To our best knowledge, this is the first finite-time analysis of neural TD that achieves an $\tilde{\mathcal{O}}(\epsilon^{-1})$ complexity under the Markovian sampling, as opposed to the best known $\tilde{\mathcal{O}}(\epsilon^{-2})$ complexity in the existing literature.