Hybrid Frequency Transmission for Upload Latency Minimization of IoT Devices in HSR Scenario Aided by Intelligent Reflecting Surfaces

The explosively growing demand for Internet of Things (IoT) in high-speed railway (HSR) scenario has attracted a lot of attention amongst researchers. However, limited IoT device (IoTD) batteries and large information upload latency still remain critical impediments to practical service applications. In this paper, we consider a HSR wireless mobile communication system, where two intelligent reflecting surfaces (IRSs) are deployed to help solve the problems above. Considering the carrier aggregation method, the IRS needs to be optimized globally in hybrid frequency bands. Meanwhile, to ensure information security, the transmission to the mobile communication relay (MCR) on the train is covert to passengers in the carriage by IRS. This problem is challenging to handle since the variables are coupled with each other and some tricky constraints. We firstly transform the original sum-of-ratios problem into the more tractable parametric problem. Then, the block coordinate descent (BCD) algorithm is adopted to decouple the problem into two main sub-problems, and the downlink and uplink settings are alternatively optimized using low-complexity iterative algorithms. Finally, a heuristic algorithm to mitigate the Doppler spread is proposed to further improve the performance. Simulation results corroborate the performance improvement of the proposed algorithm.

Monte Carlo Policy Gradient Method for Binary Optimization

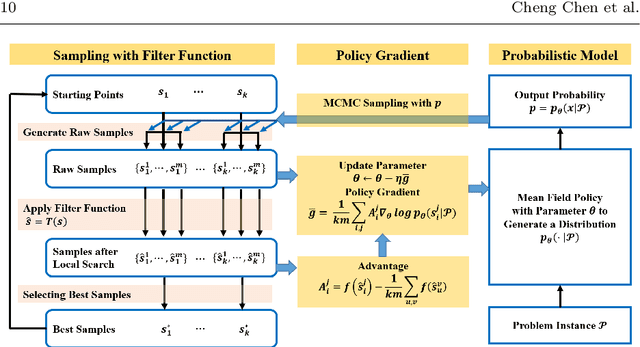
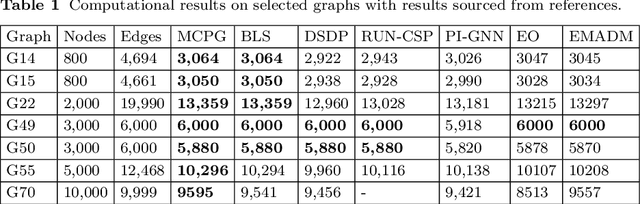
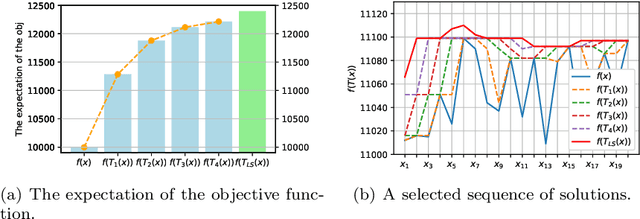
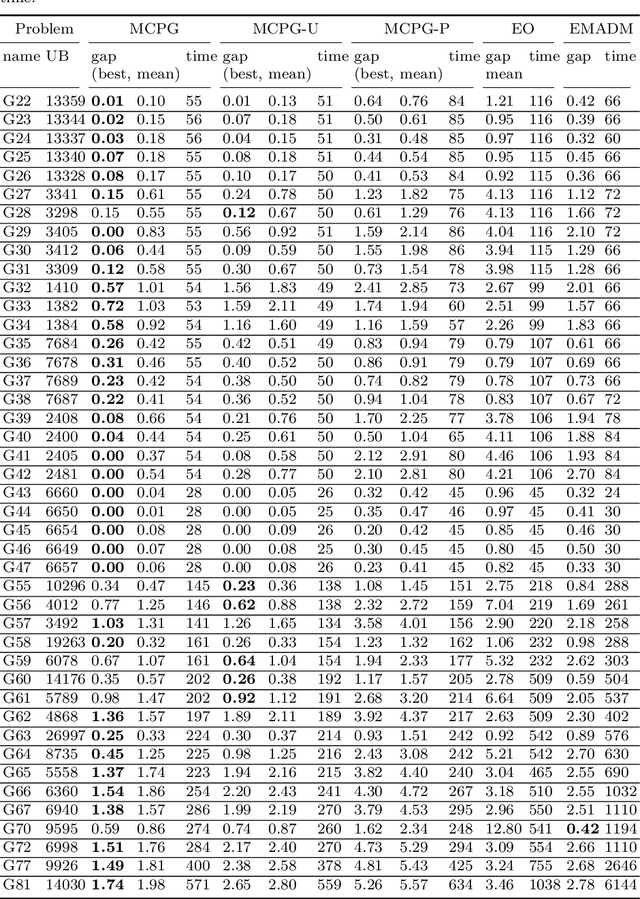
Binary optimization has a wide range of applications in combinatorial optimization problems such as MaxCut, MIMO detection, and MaxSAT. However, these problems are typically NP-hard due to the binary constraints. We develop a novel probabilistic model to sample the binary solution according to a parameterized policy distribution. Specifically, minimizing the KL divergence between the parameterized policy distribution and the Gibbs distributions of the function value leads to a stochastic optimization problem whose policy gradient can be derived explicitly similar to reinforcement learning. For coherent exploration in discrete spaces, parallel Markov Chain Monte Carlo (MCMC) methods are employed to sample from the policy distribution with diversity and approximate the gradient efficiently. We further develop a filter scheme to replace the original objective function by the one with the local search technique to broaden the horizon of the function landscape. Convergence to stationary points in expectation of the policy gradient method is established based on the concentration inequality for MCMC. Numerical results show that this framework is very promising to provide near-optimal solutions for quite a few binary optimization problems.

Provable Convergence of Variational Monte Carlo Methods

The Variational Monte Carlo (VMC) is a promising approach for computing the ground state energy of many-body quantum problems and attracts more and more interests due to the development of machine learning. The recent paradigms in VMC construct neural networks as trial wave functions, sample quantum configurations using Markov chain Monte Carlo (MCMC) and train neural networks with stochastic gradient descent (SGD) method. However, the theoretical convergence of VMC is still unknown when SGD interacts with MCMC sampling given a well-designed trial wave function. Since MCMC reduces the difficulty of estimating gradients, it has inevitable bias in practice. Moreover, the local energy may be unbounded, which makes it harder to analyze the error of MCMC sampling. Therefore, we assume that the local energy is sub-exponential and use the Bernstein inequality for non-stationary Markov chains to derive error bounds of the MCMC estimator. Consequently, VMC is proven to have a first order convergence rate $O(\log K/\sqrt{n K})$ with $K$ iterations and a sample size $n$. It partially explains how MCMC influences the behavior of SGD. Furthermore, we verify the so-called correlated negative curvature condition and relate it to the zero-variance phenomena in solving eigenvalue functions. It is shown that VMC escapes from saddle points and reaches $(\epsilon,\epsilon^{1/4})$ -approximate second order stationary points or $\epsilon^{1/2}$-variance points in at least $O(\epsilon^{-11/2}\log^{2}(1/\epsilon) )$ steps with high probability. Our analysis enriches the understanding of how VMC converges efficiently and can be applied to general variational methods in physics and statistics.

Distributed Active Noise Control System Based on a Block Diffusion FxLMS Algorithm with Bidirectional Communication

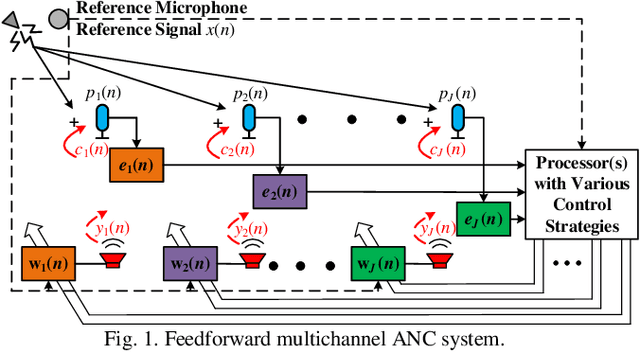
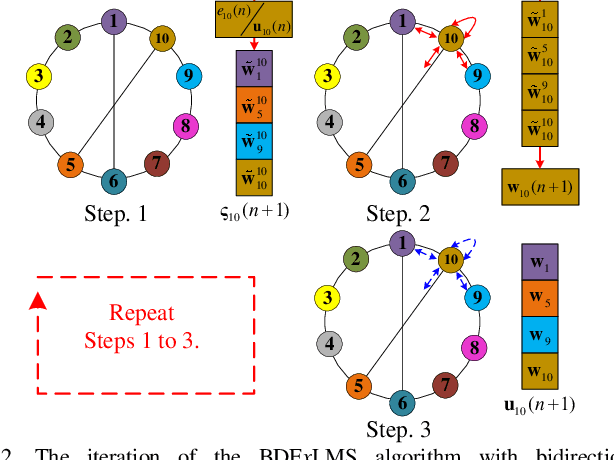
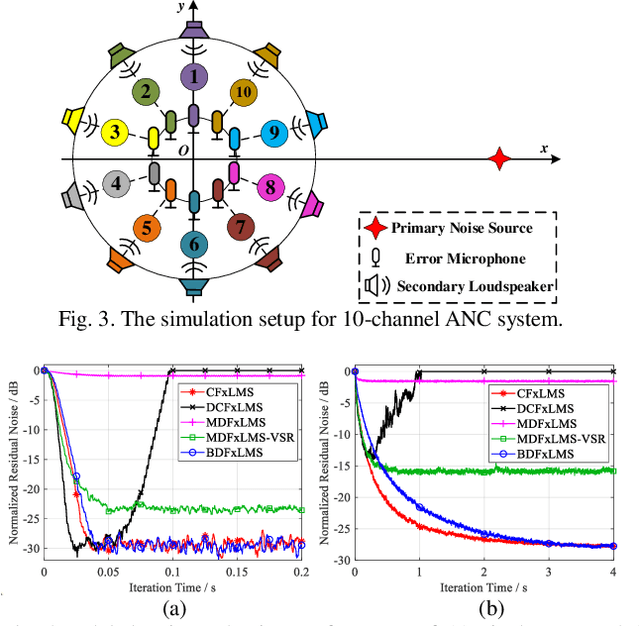
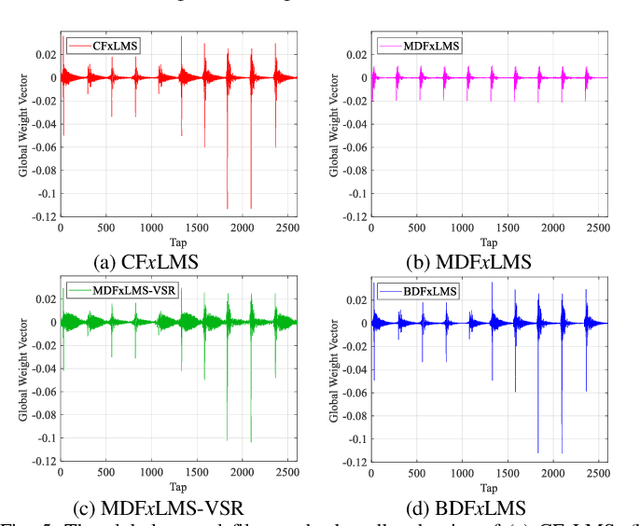
Recently, distributed active noise control systems based on diffusion adaptation have attracted significant research interest due to their balance between computational complexity and stability compared to conventional centralized and decentralized adaptation schemes. However, the existing diffusion FxLMS algorithm employs node-specific adaptation and neighborhood-wide combination, and assumes that the control filters of neighbor nodes are similar to each other. This assumption is not true in practical applications, and it leads to inferior performance to the centralized controller approach. In contrast, this paper proposes a Block Diffusion FxLMS algorithm with bidirectional communication, which uses neighborhood-wide adaptation and node-specific combination to update the control filters. Simulation results validate that the proposed algorithm converges to the solution of the centralized controller with reduced computational burden.