Accelerating Optimization via Differentiable Stopping Time

Optimization is an important module of modern machine learning applications. Tremendous efforts have been made to accelerate optimization algorithms. A common formulation is achieving a lower loss at a given time. This enables a differentiable framework with respect to the algorithm hyperparameters. In contrast, its dual, minimizing the time to reach a target loss, is believed to be non-differentiable, as the time is not differentiable. As a result, it usually serves as a conceptual framework or is optimized using zeroth-order methods. To address this limitation, we propose a differentiable stopping time and theoretically justify it based on differential equations. An efficient algorithm is designed to backpropagate through it. As a result, the proposed differentiable stopping time enables a new differentiable formulation for accelerating algorithms. We further discuss its applications, such as online hyperparameter tuning and learning to optimize. Our proposed methods show superior performance in comprehensive experiments across various problems, which confirms their effectiveness.

ODE-based Learning to Optimize

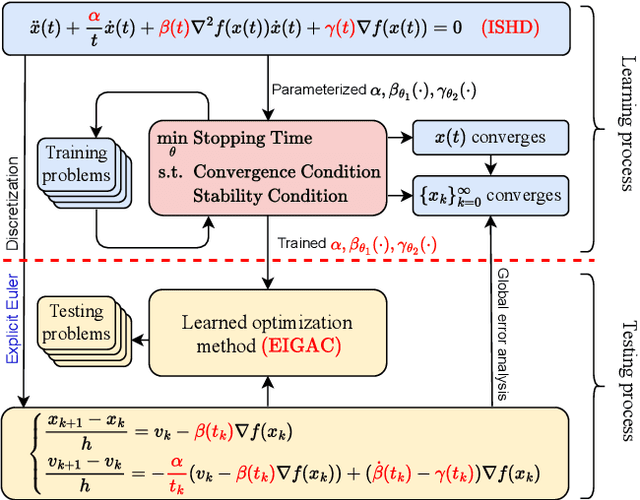
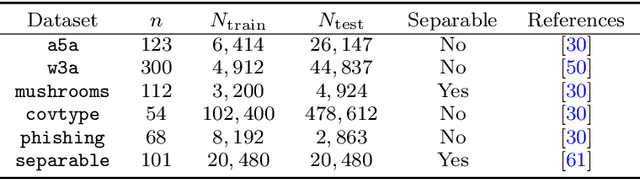
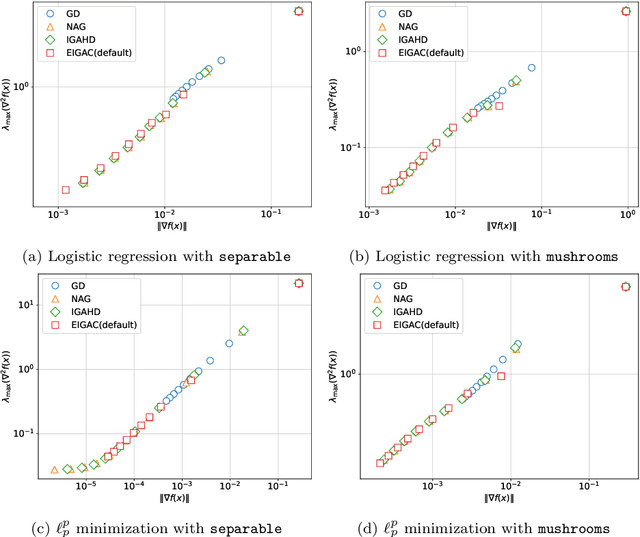
Recent years have seen a growing interest in understanding acceleration methods through the lens of ordinary differential equations (ODEs). Despite the theoretical advancements, translating the rapid convergence observed in continuous-time models to discrete-time iterative methods poses significant challenges. In this paper, we present a comprehensive framework integrating the inertial systems with Hessian-driven damping equation (ISHD) and learning-based approaches for developing optimization methods through a deep synergy of theoretical insights. We first establish the convergence condition for ensuring the convergence of the solution trajectory of ISHD. Then, we show that provided the stability condition, another relaxed requirement on the coefficients of ISHD, the sequence generated through the explicit Euler discretization of ISHD converges, which gives a large family of practical optimization methods. In order to select the best optimization method in this family for certain problems, we introduce the stopping time, the time required for an optimization method derived from ISHD to achieve a predefined level of suboptimality. Then, we formulate a novel learning to optimize (L2O) problem aimed at minimizing the stopping time subject to the convergence and stability condition. To navigate this learning problem, we present an algorithm combining stochastic optimization and the penalty method (StoPM). The convergence of StoPM using the conservative gradient is proved. Empirical validation of our framework is conducted through extensive numerical experiments across a diverse set of optimization problems. These experiments showcase the superior performance of the learned optimization methods.