Rethinking the Capacity of Graph Neural Networks for Branching Strategy

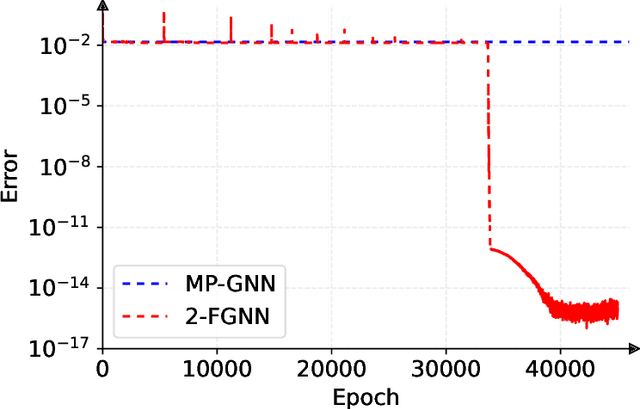
Graph neural networks (GNNs) have been widely used to predict properties and heuristics of mixed-integer linear programs (MILPs) and hence accelerate MILP solvers. This paper investigates the capacity of GNNs to represent strong branching (SB) scores that provide an efficient strategy in the branch-and-bound algorithm. Although message-passing GNN (MP-GNN), as the simplest GNN structure, is frequently employed in the existing literature to learn SB scores, we prove a fundamental limitation in its expressive power -- there exist two MILP instances with different SB scores that cannot be distinguished by any MP-GNN, regardless of the number of parameters. In addition, we establish a universal approximation theorem for another GNN structure called the second-order folklore GNN (2-FGNN). We show that for any data distribution over MILPs, there always exists a 2-FGNN that can approximate the SB score with arbitrarily high accuracy and arbitrarily high probability. A small-scale numerical experiment is conducted to directly validate our theoretical findings.