Chasing Better Deep Image Priors between Over- and Under-parameterization
Paper and Code
Oct 31, 2024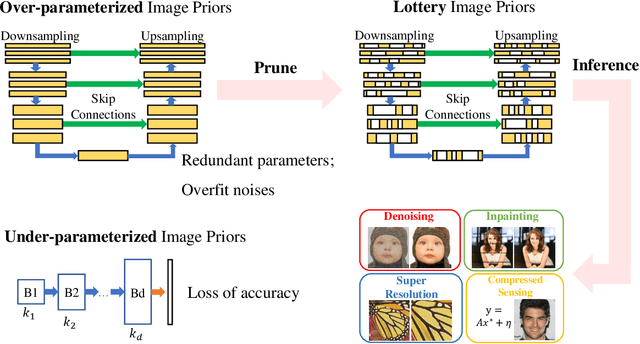


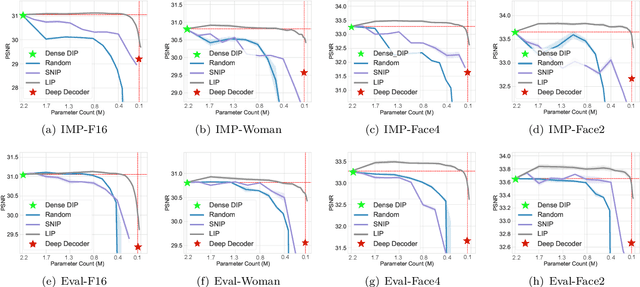
Deep Neural Networks (DNNs) are well-known to act as over-parameterized deep image priors (DIP) that regularize various image inverse problems. Meanwhile, researchers also proposed extremely compact, under-parameterized image priors (e.g., deep decoder) that are strikingly competent for image restoration too, despite a loss of accuracy. These two extremes push us to think whether there exists a better solution in the middle: between over- and under-parameterized image priors, can one identify "intermediate" parameterized image priors that achieve better trade-offs between performance, efficiency, and even preserving strong transferability? Drawing inspirations from the lottery ticket hypothesis (LTH), we conjecture and study a novel "lottery image prior" (LIP) by exploiting DNN inherent sparsity, stated as: given an over-parameterized DNN-based image prior, it will contain a sparse subnetwork that can be trained in isolation, to match the original DNN's performance when being applied as a prior to various image inverse problems. Our results validate the superiority of LIPs: we can successfully locate the LIP subnetworks from over-parameterized DIPs at substantial sparsity ranges. Those LIP subnetworks significantly outperform deep decoders under comparably compact model sizes (by often fully preserving the effectiveness of their over-parameterized counterparts), and they also possess high transferability across different images as well as restoration task types. Besides, we also extend LIP to compressive sensing image reconstruction, where a pre-trained GAN generator is used as the prior (in contrast to untrained DIP or deep decoder), and confirm its validity in this setting too. To our best knowledge, this is the first time that LTH is demonstrated to be relevant in the context of inverse problems or image priors.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge