SPLF-SAM: Self-Prompting Segment Anything Model for Light Field Salient Object Detection

Segment Anything Model (SAM) has demonstrated remarkable capabilities in solving light field salient object detection (LF SOD). However, most existing models tend to neglect the extraction of prompt information under this task. Meanwhile, traditional models ignore the analysis of frequency-domain information, which leads to small objects being overwhelmed by noise. In this paper, we put forward a novel model called self-prompting light field segment anything model (SPLF-SAM), equipped with unified multi-scale feature embedding block (UMFEB) and a multi-scale adaptive filtering adapter (MAFA). UMFEB is capable of identifying multiple objects of varying sizes, while MAFA, by learning frequency features, effectively prevents small objects from being overwhelmed by noise. Extensive experiments have demonstrated the superiority of our method over ten state-of-the-art (SOTA) LF SOD methods. Our code will be available at https://github.com/XucherCH/splfsam.

Toward Fair Federated Learning under Demographic Disparities and Data Imbalance

Ensuring fairness is critical when applying artificial intelligence to high-stakes domains such as healthcare, where predictive models trained on imbalanced and demographically skewed data risk exacerbating existing disparities. Federated learning (FL) enables privacy-preserving collaboration across institutions, but remains vulnerable to both algorithmic bias and subgroup imbalance - particularly when multiple sensitive attributes intersect. We propose FedIDA (Fed erated Learning for Imbalance and D isparity A wareness), a framework-agnostic method that combines fairness-aware regularization with group-conditional oversampling. FedIDA supports multiple sensitive attributes and heterogeneous data distributions without altering the convergence behavior of the underlying FL algorithm. We provide theoretical analysis establishing fairness improvement bounds using Lipschitz continuity and concentration inequalities, and show that FedIDA reduces the variance of fairness metrics across test sets. Empirical results on both benchmark and real-world clinical datasets confirm that FedIDA consistently improves fairness while maintaining competitive predictive performance, demonstrating its effectiveness for equitable and privacy-preserving modeling in healthcare. The source code is available on GitHub.

Chasing Better Deep Image Priors between Over- and Under-parameterization

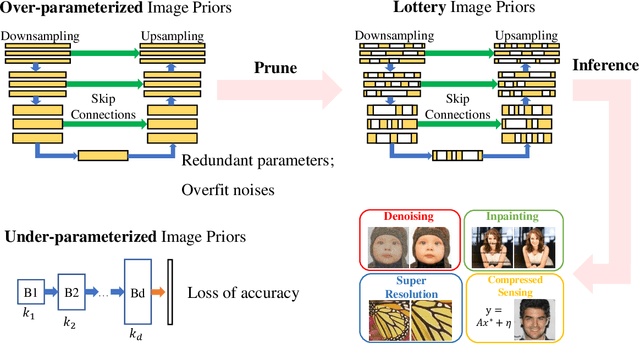
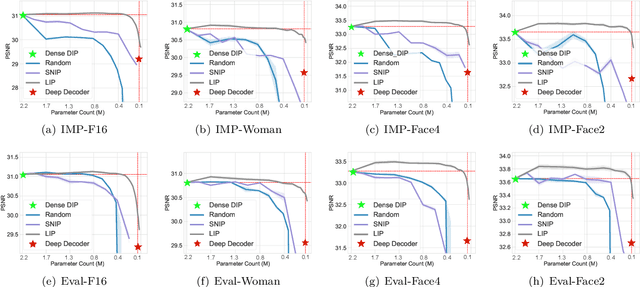
Deep Neural Networks (DNNs) are well-known to act as over-parameterized deep image priors (DIP) that regularize various image inverse problems. Meanwhile, researchers also proposed extremely compact, under-parameterized image priors (e.g., deep decoder) that are strikingly competent for image restoration too, despite a loss of accuracy. These two extremes push us to think whether there exists a better solution in the middle: between over- and under-parameterized image priors, can one identify "intermediate" parameterized image priors that achieve better trade-offs between performance, efficiency, and even preserving strong transferability? Drawing inspirations from the lottery ticket hypothesis (LTH), we conjecture and study a novel "lottery image prior" (LIP) by exploiting DNN inherent sparsity, stated as: given an over-parameterized DNN-based image prior, it will contain a sparse subnetwork that can be trained in isolation, to match the original DNN's performance when being applied as a prior to various image inverse problems. Our results validate the superiority of LIPs: we can successfully locate the LIP subnetworks from over-parameterized DIPs at substantial sparsity ranges. Those LIP subnetworks significantly outperform deep decoders under comparably compact model sizes (by often fully preserving the effectiveness of their over-parameterized counterparts), and they also possess high transferability across different images as well as restoration task types. Besides, we also extend LIP to compressive sensing image reconstruction, where a pre-trained GAN generator is used as the prior (in contrast to untrained DIP or deep decoder), and confirm its validity in this setting too. To our best knowledge, this is the first time that LTH is demonstrated to be relevant in the context of inverse problems or image priors.

Using Crank-Nikolson Scheme to Solve the Korteweg-de Vries (KdV) Equation

The Korteweg-de Vries (KdV) equation is a fundamental partial differential equation that models wave propagation in shallow water and other dispersive media. Accurately solving the KdV equation is essential for understanding wave dynamics in physics and engineering applications. This project focuses on implementing the Crank-Nicolson scheme, a finite difference method known for its stability and accuracy, to solve the KdV equation. The Crank-Nicolson scheme's implicit nature allows for a more stable numerical solution, especially in handling the dispersive and nonlinear terms of the KdV equation. We investigate the performance of the scheme through various test cases, analyzing its convergence and error behavior. The results demonstrate that the Crank-Nicolson method provides a robust approach for solving the KdV equation, with improved accuracy over traditional explicit methods. Code is available at the end of the paper.

Bound Tightening Network for Robust Crowd Counting

Crowd Counting is a fundamental topic, aiming to estimate the number of individuals in the crowded images or videos fed from surveillance cameras. Recent works focus on improving counting accuracy, while ignoring the certified robustness of counting models. In this paper, we propose a novel Bound Tightening Network (BTN) for Robust Crowd Counting. It consists of three parts: base model, smooth regularization module and certify bound module. The core idea is to propagate the interval bound through the base model (certify bound module) and utilize the layer weights (smooth regularization module) to guide the network learning. Experiments on different benchmark datasets for counting demonstrate the effectiveness and efficiency of BTN.

GraphEval2000: Benchmarking and Improving Large Language Models on Graph Datasets

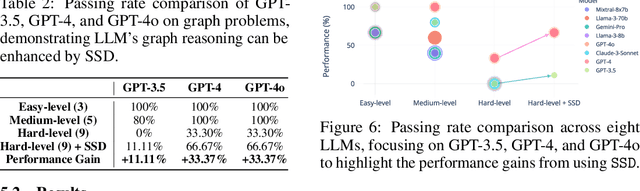
Large language models (LLMs) have achieved remarkable success in natural language processing (NLP), demonstrating significant capabilities in processing and understanding text data. However, recent studies have identified limitations in LLMs' ability to reason about graph-structured data. To address this gap, we introduce GraphEval2000, the first comprehensive graph dataset, comprising 40 graph data structure problems along with 2000 test cases. Additionally, we introduce an evaluation framework based on GraphEval2000, designed to assess the graph reasoning abilities of LLMs through coding challenges. Our dataset categorizes test cases into four primary and four sub-categories, ensuring a comprehensive evaluation. We evaluate eight popular LLMs on GraphEval2000, revealing that LLMs exhibit a better understanding of directed graphs compared to undirected ones. While private LLMs consistently outperform open-source models, the performance gap is narrowing. Furthermore, to improve the usability of our evaluation framework, we propose Structured Symbolic Decomposition (SSD), an instruction-based method designed to enhance LLM performance on GraphEval2000. Results show that SSD improves the performance of GPT-3.5, GPT-4, and GPT-4o on complex graph problems, with an increase of 11.11\%, 33.37\%, and 33.37\%, respectively.

Developing Federated Time-to-Event Scores Using Heterogeneous Real-World Survival Data

Survival analysis serves as a fundamental component in numerous healthcare applications, where the determination of the time to specific events (such as the onset of a certain disease or death) for patients is crucial for clinical decision-making. Scoring systems are widely used for swift and efficient risk prediction. However, existing methods for constructing survival scores presume that data originates from a single source, posing privacy challenges in collaborations with multiple data owners. We propose a novel framework for building federated scoring systems for multi-site survival outcomes, ensuring both privacy and communication efficiency. We applied our approach to sites with heterogeneous survival data originating from emergency departments in Singapore and the United States. Additionally, we independently developed local scores at each site. In testing datasets from each participant site, our proposed federated scoring system consistently outperformed all local models, evidenced by higher integrated area under the receiver operating characteristic curve (iAUC) values, with a maximum improvement of 11.6%. Additionally, the federated score's time-dependent AUC(t) values showed advantages over local scores, exhibiting narrower confidence intervals (CIs) across most time points. The model developed through our proposed method exhibits effective performance on each local site, signifying noteworthy implications for healthcare research. Sites participating in our proposed federated scoring model training gained benefits by acquiring survival models with enhanced prediction accuracy and efficiency. This study demonstrates the effectiveness of our privacy-preserving federated survival score generation framework and its applicability to real-world heterogeneous survival data.

Federated Learning for Clinical Structured Data: A Benchmark Comparison of Engineering and Statistical Approaches

Federated learning (FL) has shown promising potential in safeguarding data privacy in healthcare collaborations. While the term "FL" was originally coined by the engineering community, the statistical field has also explored similar privacy-preserving algorithms. Statistical FL algorithms, however, remain considerably less recognized than their engineering counterparts. Our goal was to bridge the gap by presenting the first comprehensive comparison of FL frameworks from both engineering and statistical domains. We evaluated five FL frameworks using both simulated and real-world data. The results indicate that statistical FL algorithms yield less biased point estimates for model coefficients and offer convenient confidence interval estimations. In contrast, engineering-based methods tend to generate more accurate predictions, sometimes surpassing central pooled and statistical FL models. This study underscores the relative strengths and weaknesses of both types of methods, emphasizing the need for increased awareness and their integration in future FL applications.

Towards Adversarial Patch Analysis and Certified Defense against Crowd Counting

Crowd counting has drawn much attention due to its importance in safety-critical surveillance systems. Especially, deep neural network (DNN) methods have significantly reduced estimation errors for crowd counting missions. Recent studies have demonstrated that DNNs are vulnerable to adversarial attacks, i.e., normal images with human-imperceptible perturbations could mislead DNNs to make false predictions. In this work, we propose a robust attack strategy called Adversarial Patch Attack with Momentum (APAM) to systematically evaluate the robustness of crowd counting models, where the attacker's goal is to create an adversarial perturbation that severely degrades their performances, thus leading to public safety accidents (e.g., stampede accidents). Especially, the proposed attack leverages the extreme-density background information of input images to generate robust adversarial patches via a series of transformations (e.g., interpolation, rotation, etc.). We observe that by perturbing less than 6\% of image pixels, our attacks severely degrade the performance of crowd counting systems, both digitally and physically. To better enhance the adversarial robustness of crowd counting models, we propose the first regression model-based Randomized Ablation (RA), which is more sufficient than Adversarial Training (ADT) (Mean Absolute Error of RA is 5 lower than ADT on clean samples and 30 lower than ADT on adversarial examples). Extensive experiments on five crowd counting models demonstrate the effectiveness and generality of the proposed method. Code is available at \url{https://github.com/harrywuhust2022/Adv-Crowd-analysis}.