More ConvNets in the 2020s: Scaling up Kernels Beyond 51x51 using Sparsity

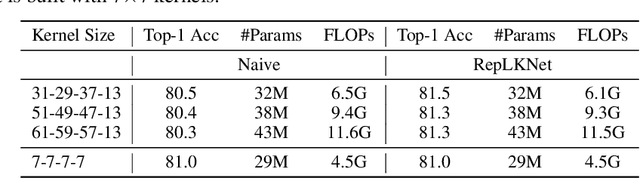
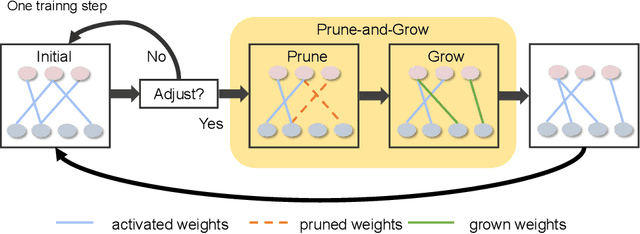
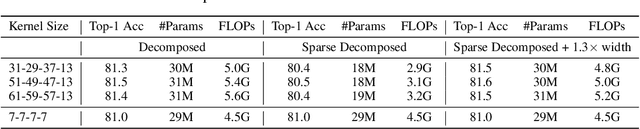
Transformers have quickly shined in the computer vision world since the emergence of Vision Transformers (ViTs). The dominant role of convolutional neural networks (CNNs) seems to be challenged by increasingly effective transformer-based models. Very recently, a couple of advanced convolutional models strike back with large kernels motivated by the local but large attention mechanism, showing appealing performance and efficiency. While one of them, i.e. RepLKNet, impressively manages to scale the kernel size to 31x31 with improved performance, the performance starts to saturate as the kernel size continues growing, compared to the scaling trend of advanced ViTs such as Swin Transformer. In this paper, we explore the possibility of training extreme convolutions larger than 31x31 and test whether the performance gap can be eliminated by strategically enlarging convolutions. This study ends up with a recipe for applying extremely large kernels from the perspective of sparsity, which can smoothly scale up kernels to 61x61 with better performance. Built on this recipe, we propose Sparse Large Kernel Network (SLaK), a pure CNN architecture equipped with 51x51 kernels that can perform on par with or better than state-of-the-art hierarchical Transformers and modern ConvNet architectures like ConvNeXt and RepLKNet, on ImageNet classification as well as typical downstream tasks. Our code is available here https://github.com/VITA-Group/SLaK.

Softmax-based Classification is k-means Clustering: Formal Proof, Consequences for Adversarial Attacks, and Improvement through Centroid Based Tailoring

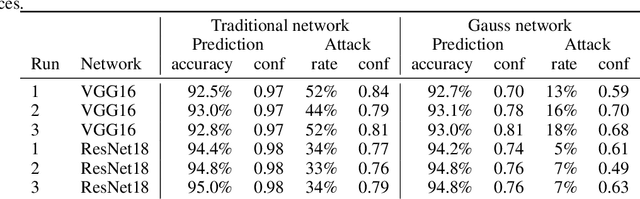
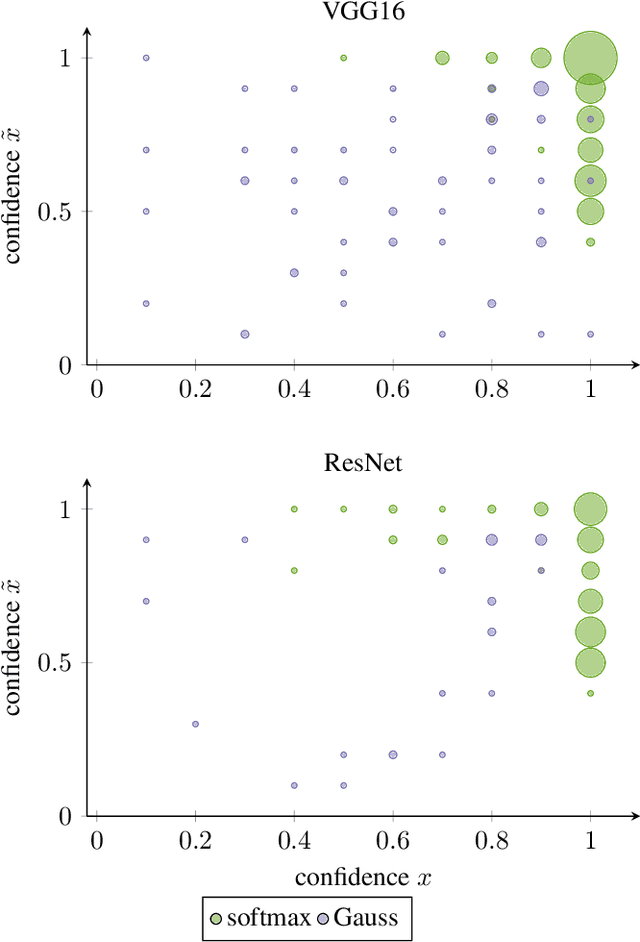
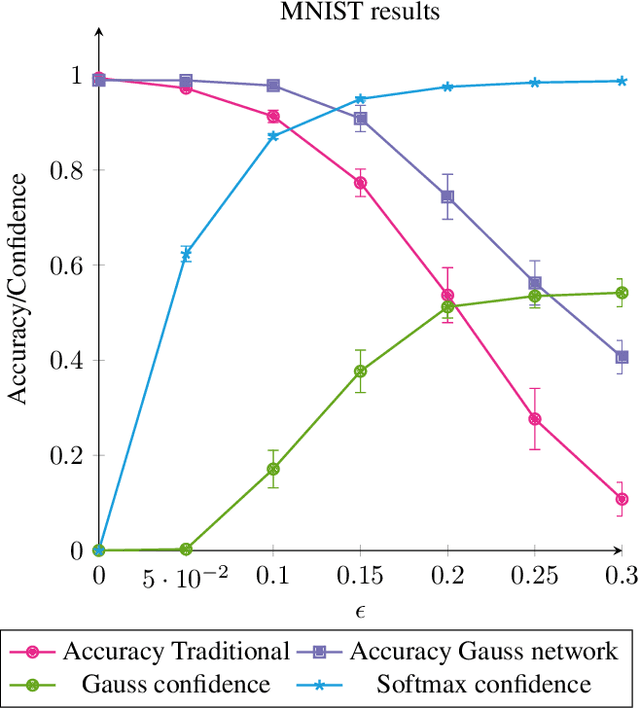
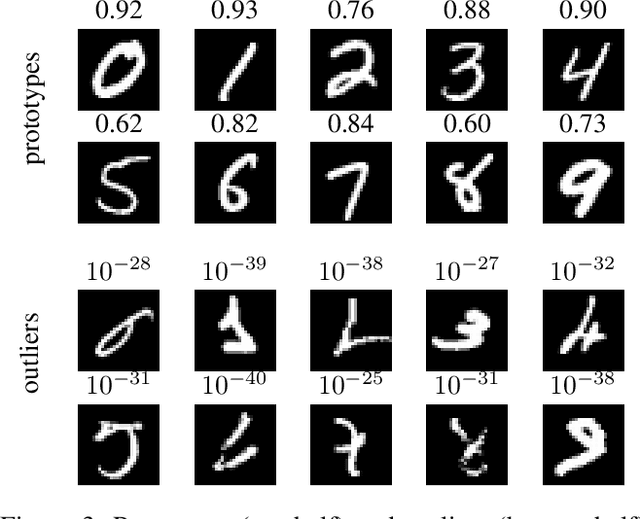
We formally prove the connection between k-means clustering and the predictions of neural networks based on the softmax activation layer. In existing work, this connection has been analyzed empirically, but it has never before been mathematically derived. The softmax function partitions the transformed input space into cones, each of which encompasses a class. This is equivalent to putting a number of centroids in this transformed space at equal distance from the origin, and k-means clustering the data points by proximity to these centroids. Softmax only cares in which cone a data point falls, and not how far from the centroid it is within that cone. We formally prove that networks with a small Lipschitz modulus (which corresponds to a low susceptibility to adversarial attacks) map data points closer to the cluster centroids, which results in a mapping to a k-means-friendly space. To leverage this knowledge, we propose Centroid Based Tailoring as an alternative to the softmax function in the last layer of a neural network. The resulting Gauss network has similar predictive accuracy as traditional networks, but is less susceptible to one-pixel attacks; while the main contribution of this paper is theoretical in nature, the Gauss network contributes empirical auxiliary benefits.