Beyond Discriminant Patterns: On the Robustness of Decision Rule Ensembles

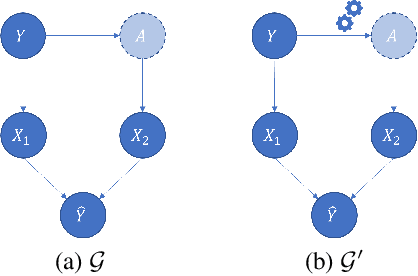
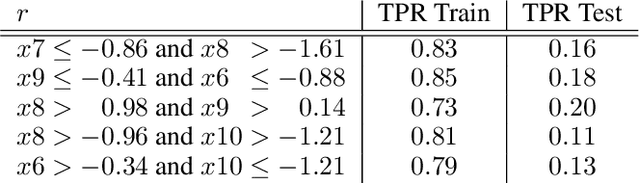
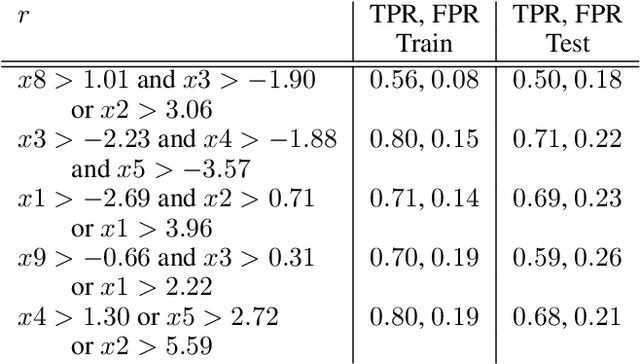
Local decision rules are commonly understood to be more explainable, due to the local nature of the patterns involved. With numerical optimization methods such as gradient boosting, ensembles of local decision rules can gain good predictive performance on data involving global structure. Meanwhile, machine learning models are being increasingly used to solve problems in high-stake domains including healthcare and finance. Here, there is an emerging consensus regarding the need for practitioners to understand whether and how those models could perform robustly in the deployment environments, in the presence of distributional shifts. Past research on local decision rules has focused mainly on maximizing discriminant patterns, without due consideration of robustness against distributional shifts. In order to fill this gap, we propose a new method to learn and ensemble local decision rules, that are robust both in the training and deployment environments. Specifically, we propose to leverage causal knowledge by regarding the distributional shifts in subpopulations and deployment environments as the results of interventions on the underlying system. We propose two regularization terms based on causal knowledge to search for optimal and stable rules. Experiments on both synthetic and benchmark datasets show that our method is effective and robust against distributional shifts in multiple environments.

Softmax-based Classification is k-means Clustering: Formal Proof, Consequences for Adversarial Attacks, and Improvement through Centroid Based Tailoring

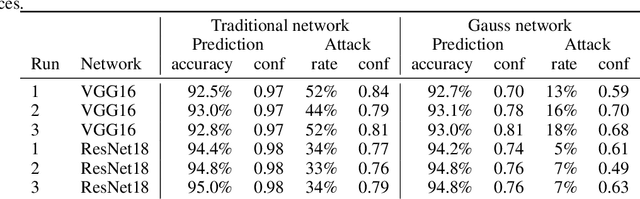
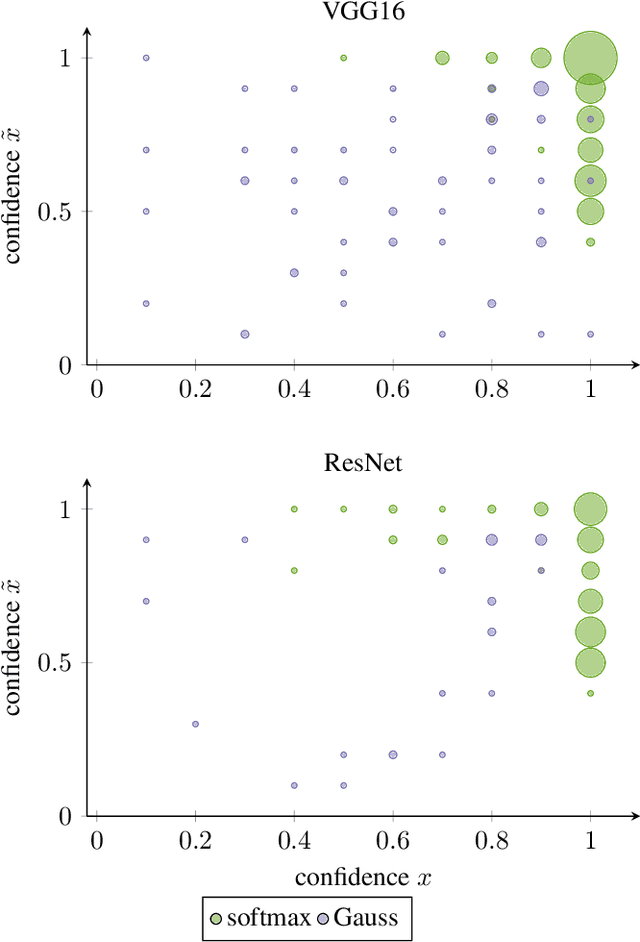
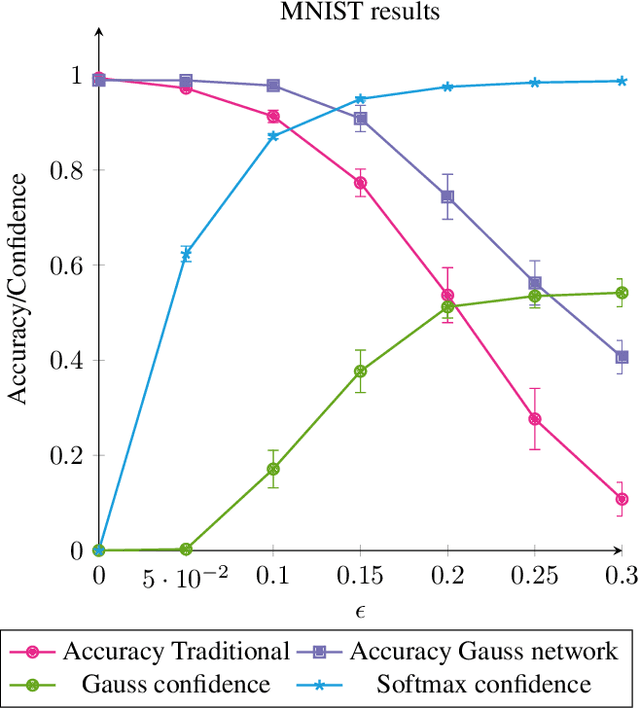
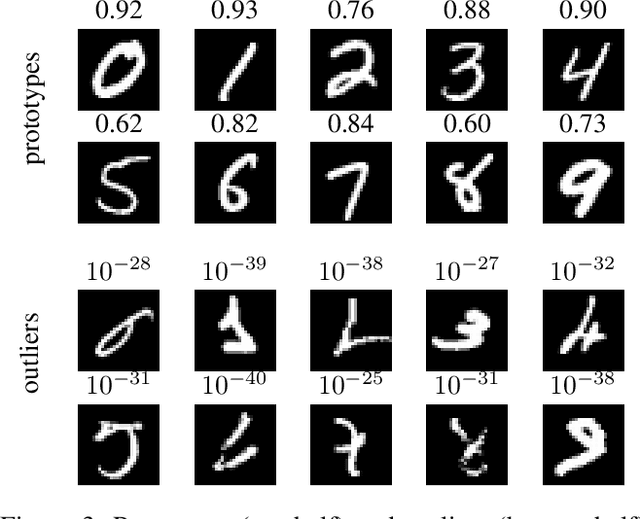
We formally prove the connection between k-means clustering and the predictions of neural networks based on the softmax activation layer. In existing work, this connection has been analyzed empirically, but it has never before been mathematically derived. The softmax function partitions the transformed input space into cones, each of which encompasses a class. This is equivalent to putting a number of centroids in this transformed space at equal distance from the origin, and k-means clustering the data points by proximity to these centroids. Softmax only cares in which cone a data point falls, and not how far from the centroid it is within that cone. We formally prove that networks with a small Lipschitz modulus (which corresponds to a low susceptibility to adversarial attacks) map data points closer to the cluster centroids, which results in a mapping to a k-means-friendly space. To leverage this knowledge, we propose Centroid Based Tailoring as an alternative to the softmax function in the last layer of a neural network. The resulting Gauss network has similar predictive accuracy as traditional networks, but is less susceptible to one-pixel attacks; while the main contribution of this paper is theoretical in nature, the Gauss network contributes empirical auxiliary benefits.

k is the Magic Number -- Inferring the Number of Clusters Through Nonparametric Concentration Inequalities

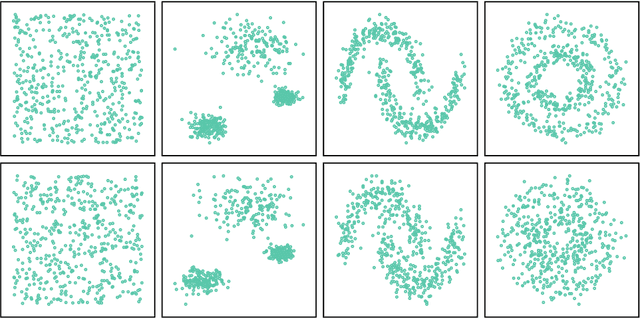
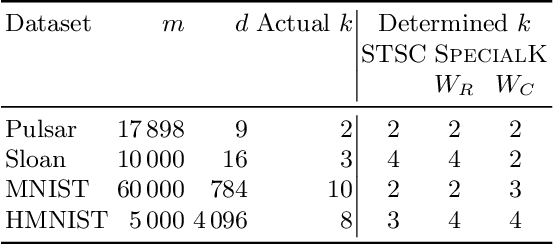
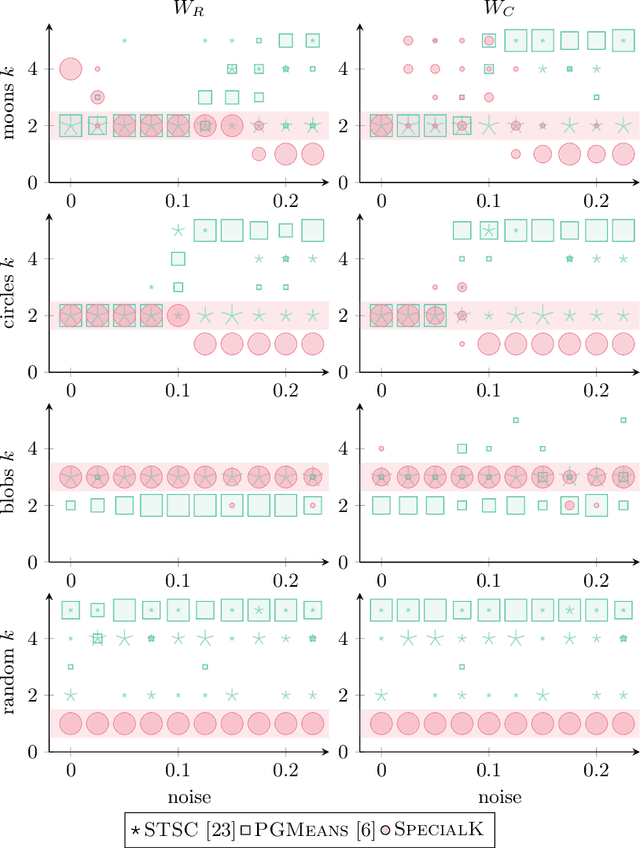
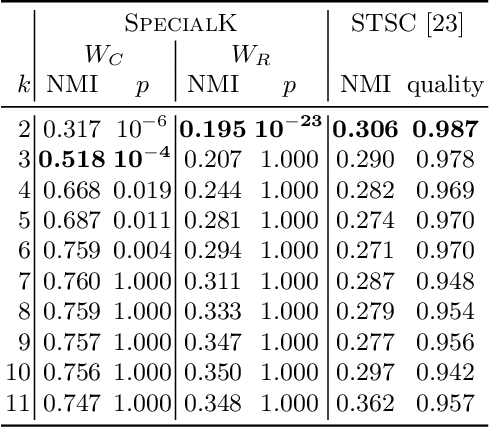
Most convex and nonconvex clustering algorithms come with one crucial parameter: the $k$ in $k$-means. To this day, there is not one generally accepted way to accurately determine this parameter. Popular methods are simple yet theoretically unfounded, such as searching for an elbow in the curve of a given cost measure. In contrast, statistically founded methods often make strict assumptions over the data distribution or come with their own optimization scheme for the clustering objective. This limits either the set of applicable datasets or clustering algorithms. In this paper, we strive to determine the number of clusters by answering a simple question: given two clusters, is it likely that they jointly stem from a single distribution? To this end, we propose a bound on the probability that two clusters originate from the distribution of the unified cluster, specified only by the sample mean and variance. Our method is applicable as a simple wrapper to the result of any clustering method minimizing the objective of $k$-means, which includes Gaussian mixtures and Spectral Clustering. We focus in our experimental evaluation on an application for nonconvex clustering and demonstrate the suitability of our theoretical results. Our \textsc{SpecialK} clustering algorithm automatically determines the appropriate value for $k$, without requiring any data transformation or projection, and without assumptions on the data distribution. Additionally, it is capable to decide that the data consists of only a single cluster, which many existing algorithms cannot.

The SpectACl of Nonconvex Clustering: A Spectral Approach to Density-Based Clustering

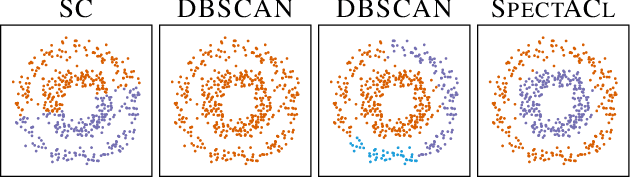
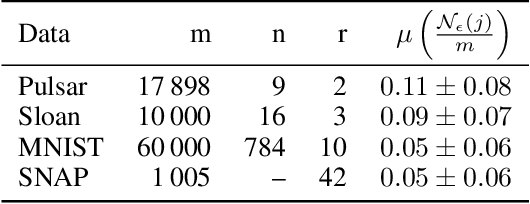
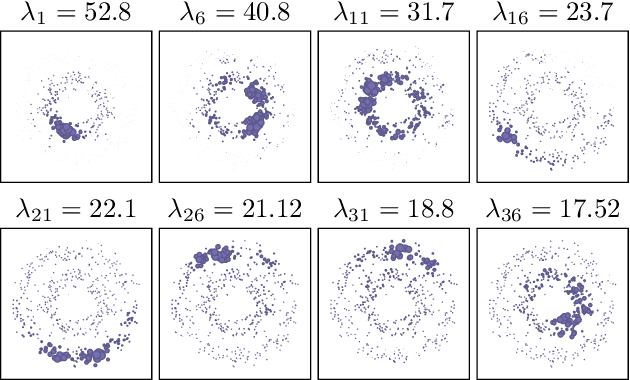
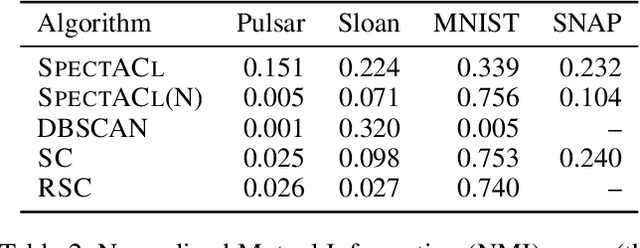
When it comes to clustering nonconvex shapes, two paradigms are used to find the most suitable clustering: minimum cut and maximum density. The most popular algorithms incorporating these paradigms are Spectral Clustering and DBSCAN. Both paradigms have their pros and cons. While minimum cut clusterings are sensitive to noise, density-based clusterings have trouble handling clusters with varying densities. In this paper, we propose \textsc{SpectACl}: a method combining the advantages of both approaches, while solving the two mentioned drawbacks. Our method is easy to implement, such as spectral clustering, and theoretically founded to optimize a proposed density criterion of clusterings. Through experiments on synthetic and real-world data, we demonstrate that our approach provides robust and reliable clusterings.

Adversarial Balancing-based Representation Learning for Causal Effect Inference with Observational Data

Learning causal effects from observational data greatly benefits a variety of domains such as healthcare, education and sociology. For instance, one could estimate the impact of a policy to decrease unemployment rate. The central problem for causal effect inference is dealing with the unobserved counterfactuals and treatment selection bias. The state-of-the-art approaches focus on solving these problems by balancing the treatment and control groups. However, during the learning and balancing process, highly predictive information from the original covariate space might be lost. In order to build more robust estimators, we tackle this information loss problem by presenting a method called Adversarial Balancing-based representation learning for Causal Effect Inference (ABCEI), based on the recent advances in deep learning. ABCEI uses adversarial learning to balance the distributions of treatment and control group in the latent representation space, without any assumption on the form of the treatment selection/assignment function. ABCEI preserves useful information for predicting causal effects under the regularization of a mutual information estimator. We conduct various experiments on several synthetic and real-world datasets. The experimental results show that ABCEI is robust against treatment selection bias, and matches/outperforms the state-of-the-art approaches.

Controversy Rules - Discovering Regions Where Classifiers (Dis-)Agree Exceptionally

Finding regions for which there is higher controversy among different classifiers is insightful with regards to the domain and our models. Such evaluation can falsify assumptions, assert some, or also, bring to the attention unknown phenomena. The present work describes an algorithm, which is based on the Exceptional Model Mining framework, and enables that kind of investigations. We explore several public datasets and show the usefulness of this approach in classification tasks. We show in this paper a few interesting observations about those well explored datasets, some of which are general knowledge, and other that as far as we know, were not reported before.

Subjectively Interesting Subgroup Discovery on Real-valued Targets

Deriving insights from high-dimensional data is one of the core problems in data mining. The difficulty mainly stems from the fact that there are exponentially many variable combinations to potentially consider, and there are infinitely many if we consider weighted combinations, even for linear combinations. Hence, an obvious question is whether we can automate the search for interesting patterns and visualizations. In this paper, we consider the setting where a user wants to learn as efficiently as possible about real-valued attributes. For example, to understand the distribution of crime rates in different geographic areas in terms of other (numerical, ordinal and/or categorical) variables that describe the areas. We introduce a method to find subgroups in the data that are maximally informative (in the formal Information Theoretic sense) with respect to a single or set of real-valued target attributes. The subgroup descriptions are in terms of a succinct set of arbitrarily-typed other attributes. The approach is based on the Subjective Interestingness framework FORSIED to enable the use of prior knowledge when finding most informative non-redundant patterns, and hence the method also supports iterative data mining.