Scoring rule nets: beyond mean target prediction in multivariate regression

Probabilistic regression models trained with maximum likelihood estimation (MLE), can sometimes overestimate variance to an unacceptable degree. This is mostly problematic in the multivariate domain. While univariate models often optimize the popular Continuous Ranked Probability Score (CRPS), in the multivariate domain, no such alternative to MLE has yet been widely accepted. The Energy Score - the most investigated alternative - notoriously lacks closed-form expressions and sensitivity to the correlation between target variables. In this paper, we propose Conditional CRPS: a multivariate strictly proper scoring rule that extends CRPS. We show that closed-form expressions exist for popular distributions and illustrate their sensitivity to correlation. We then show in a variety of experiments on both synthetic and real data, that Conditional CRPS often outperforms MLE, and produces results comparable to state-of-the-art non-parametric models, such as Distributional Random Forest (DRF).

Shrub Ensembles for Online Classification

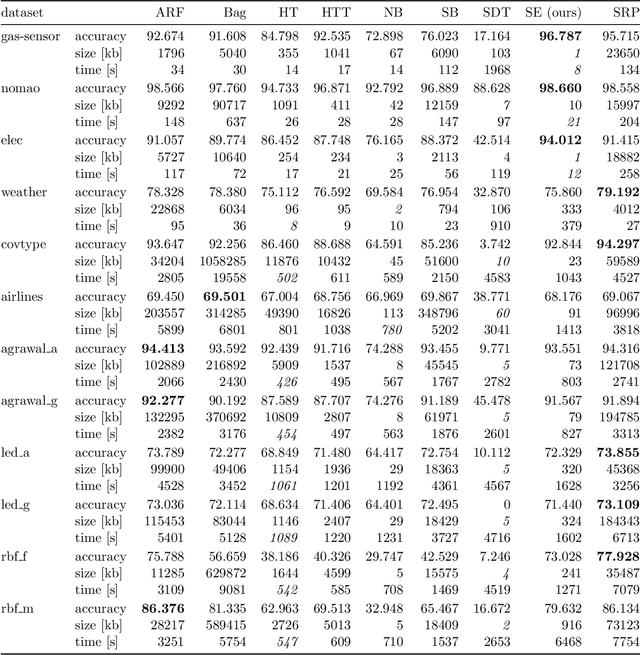
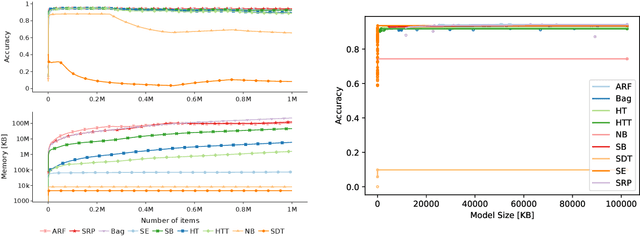
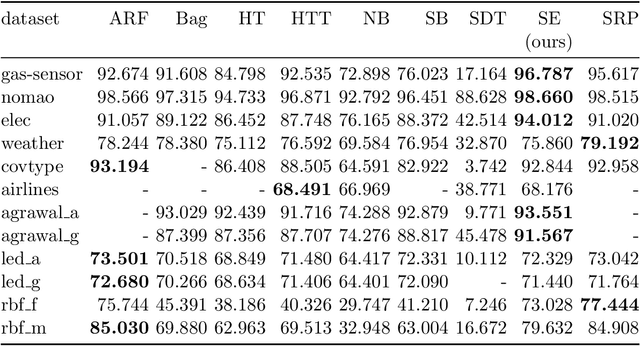
Online learning algorithms have become a ubiquitous tool in the machine learning toolbox and are frequently used in small, resource-constraint environments. Among the most successful online learning methods are Decision Tree (DT) ensembles. DT ensembles provide excellent performance while adapting to changes in the data, but they are not resource efficient. Incremental tree learners keep adding new nodes to the tree but never remove old ones increasing the memory consumption over time. Gradient-based tree learning, on the other hand, requires the computation of gradients over the entire tree which is costly for even moderately sized trees. In this paper, we propose a novel memory-efficient online classification ensemble called shrub ensembles for resource-constraint systems. Our algorithm trains small to medium-sized decision trees on small windows and uses stochastic proximal gradient descent to learn the ensemble weights of these `shrubs'. We provide a theoretical analysis of our algorithm and include an extensive discussion on the behavior of our approach in the online setting. In a series of 2~959 experiments on 12 different datasets, we compare our method against 8 state-of-the-art methods. Our Shrub Ensembles retain an excellent performance even when only little memory is available. We show that SE offers a better accuracy-memory trade-off in 7 of 12 cases, while having a statistically significant better performance than most other methods. Our implementation is available under https://github.com/sbuschjaeger/se-online .

Softmax-based Classification is k-means Clustering: Formal Proof, Consequences for Adversarial Attacks, and Improvement through Centroid Based Tailoring

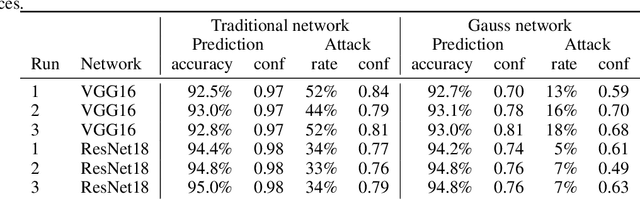
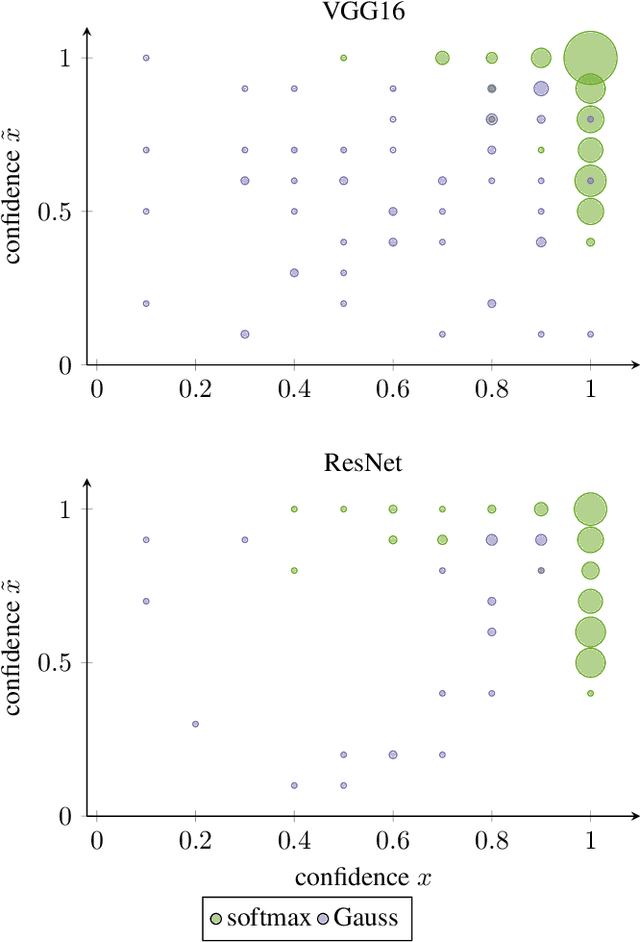
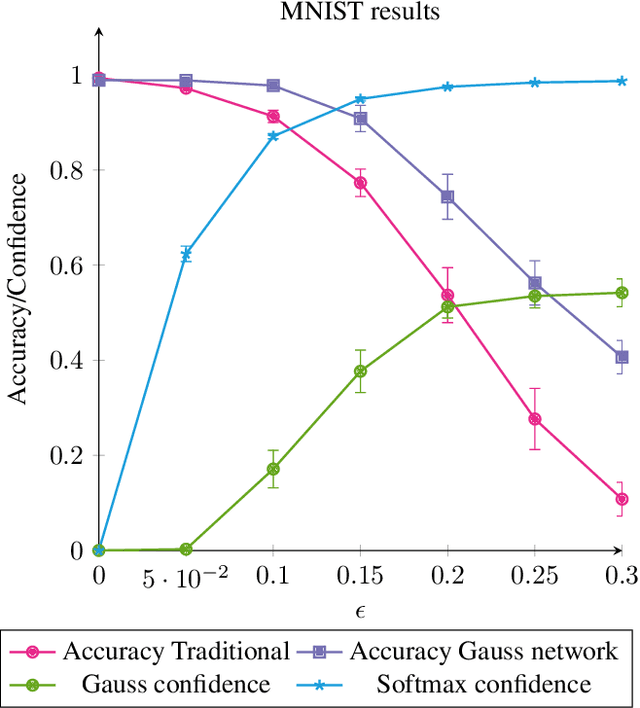
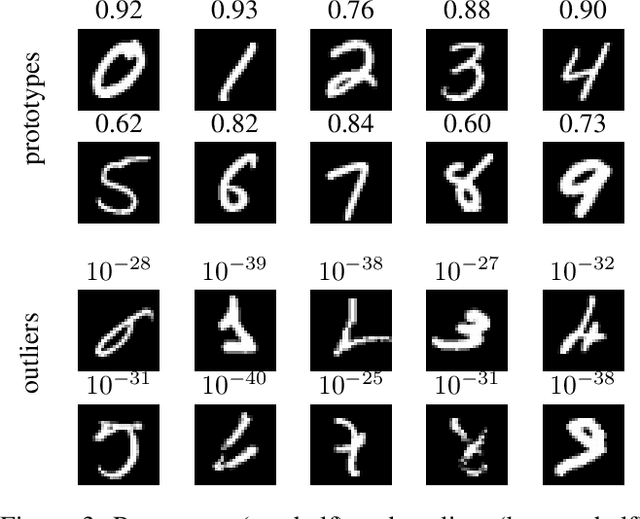
We formally prove the connection between k-means clustering and the predictions of neural networks based on the softmax activation layer. In existing work, this connection has been analyzed empirically, but it has never before been mathematically derived. The softmax function partitions the transformed input space into cones, each of which encompasses a class. This is equivalent to putting a number of centroids in this transformed space at equal distance from the origin, and k-means clustering the data points by proximity to these centroids. Softmax only cares in which cone a data point falls, and not how far from the centroid it is within that cone. We formally prove that networks with a small Lipschitz modulus (which corresponds to a low susceptibility to adversarial attacks) map data points closer to the cluster centroids, which results in a mapping to a k-means-friendly space. To leverage this knowledge, we propose Centroid Based Tailoring as an alternative to the softmax function in the last layer of a neural network. The resulting Gauss network has similar predictive accuracy as traditional networks, but is less susceptible to one-pixel attacks; while the main contribution of this paper is theoretical in nature, the Gauss network contributes empirical auxiliary benefits.

k is the Magic Number -- Inferring the Number of Clusters Through Nonparametric Concentration Inequalities

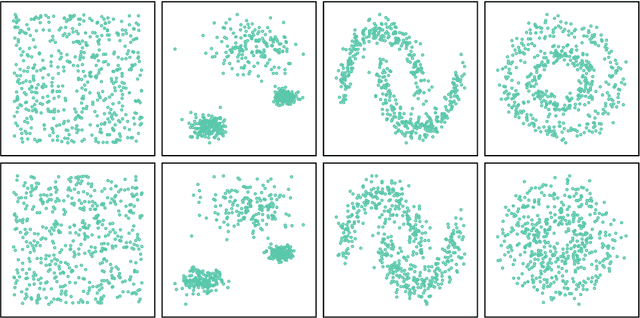
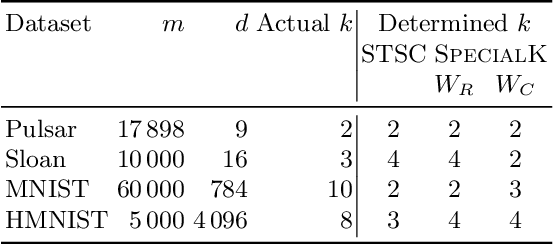
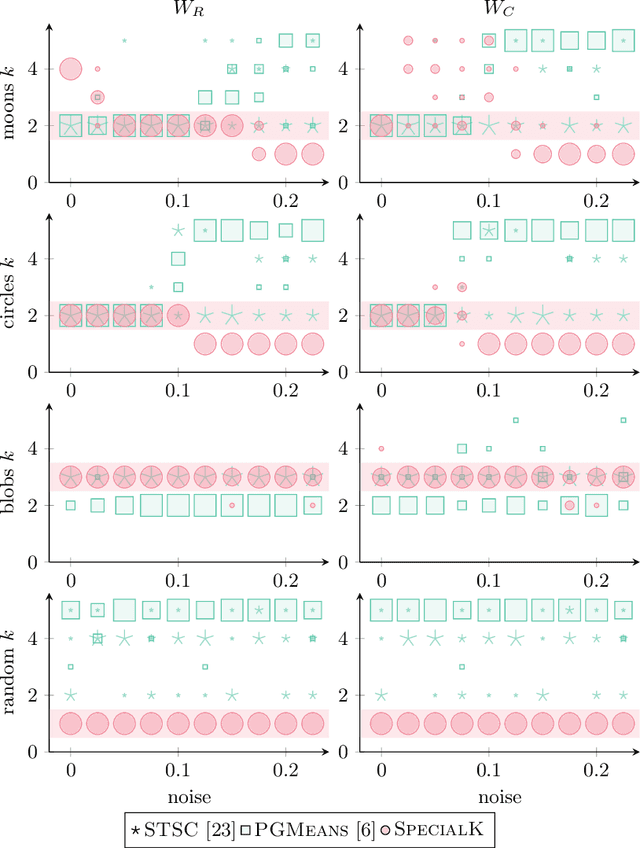
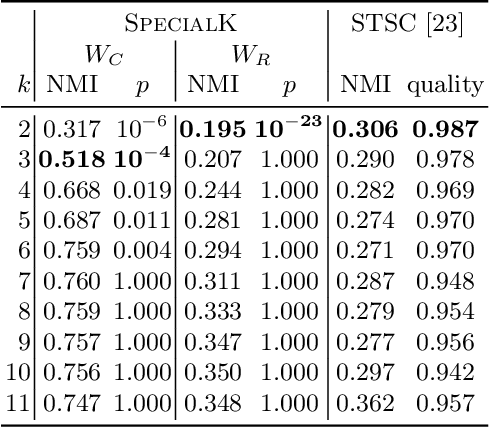
Most convex and nonconvex clustering algorithms come with one crucial parameter: the $k$ in $k$-means. To this day, there is not one generally accepted way to accurately determine this parameter. Popular methods are simple yet theoretically unfounded, such as searching for an elbow in the curve of a given cost measure. In contrast, statistically founded methods often make strict assumptions over the data distribution or come with their own optimization scheme for the clustering objective. This limits either the set of applicable datasets or clustering algorithms. In this paper, we strive to determine the number of clusters by answering a simple question: given two clusters, is it likely that they jointly stem from a single distribution? To this end, we propose a bound on the probability that two clusters originate from the distribution of the unified cluster, specified only by the sample mean and variance. Our method is applicable as a simple wrapper to the result of any clustering method minimizing the objective of $k$-means, which includes Gaussian mixtures and Spectral Clustering. We focus in our experimental evaluation on an application for nonconvex clustering and demonstrate the suitability of our theoretical results. Our \textsc{SpecialK} clustering algorithm automatically determines the appropriate value for $k$, without requiring any data transformation or projection, and without assumptions on the data distribution. Additionally, it is capable to decide that the data consists of only a single cluster, which many existing algorithms cannot.

The Trustworthy Pal: Controlling the False Discovery Rate in Boolean Matrix Factorization

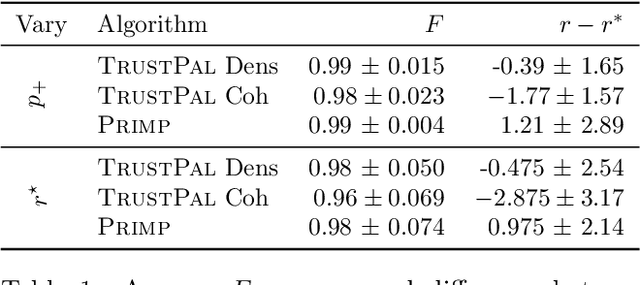
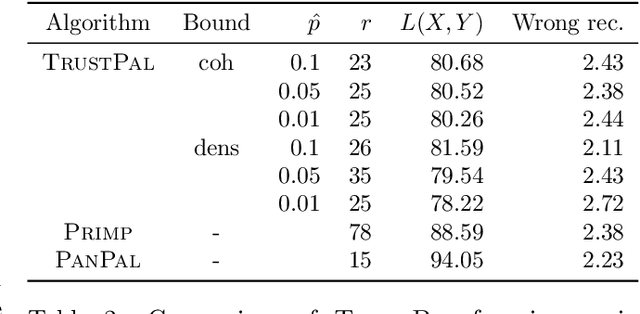
Boolean matrix factorization (BMF) is a popular and powerful technique for inferring knowledge from data. The mining result is the Boolean product of two matrices, approximating the input dataset. The Boolean product is a disjunction of rank-1 binary matrices, each describing a feature-relation, called pattern, for a group of samples. Yet, there are no guarantees that any of the returned patterns do not actually arise from noise, i.e., are false discoveries. In this paper, we propose and discuss the usage of the false discovery rate in the unsupervised BMF setting. We prove two bounds on the probability that a found pattern is constituted of random Bernoulli-distributed noise. Each bound exploits a specific property of the factorization which minimizes the approximation error---yielding new insights on the minimizers of Boolean matrix factorization. This leads to improved BMF algorithms by replacing heuristic rank selection techniques with a theoretically well-based approach. Our empirical demonstration shows that both bounds deliver excellent results in various practical settings.

The SpectACl of Nonconvex Clustering: A Spectral Approach to Density-Based Clustering

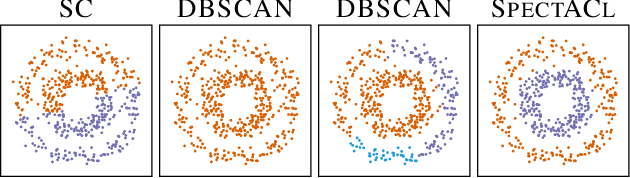
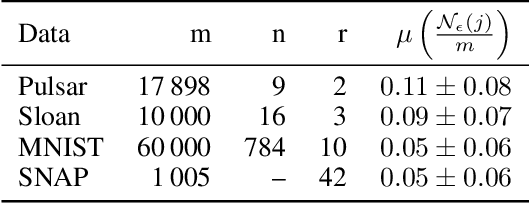
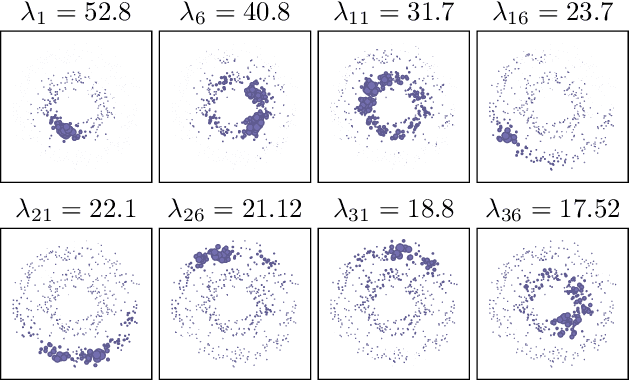
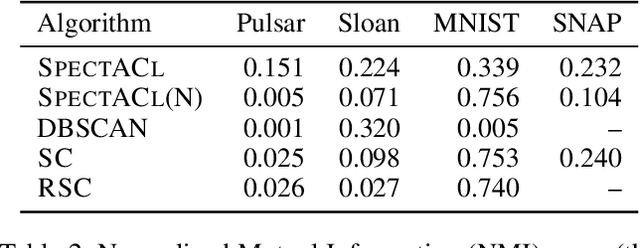
When it comes to clustering nonconvex shapes, two paradigms are used to find the most suitable clustering: minimum cut and maximum density. The most popular algorithms incorporating these paradigms are Spectral Clustering and DBSCAN. Both paradigms have their pros and cons. While minimum cut clusterings are sensitive to noise, density-based clusterings have trouble handling clusters with varying densities. In this paper, we propose \textsc{SpectACl}: a method combining the advantages of both approaches, while solving the two mentioned drawbacks. Our method is easy to implement, such as spectral clustering, and theoretically founded to optimize a proposed density criterion of clusterings. Through experiments on synthetic and real-world data, we demonstrate that our approach provides robust and reliable clusterings.

C-SALT: Mining Class-Specific ALTerations in Boolean Matrix Factorization

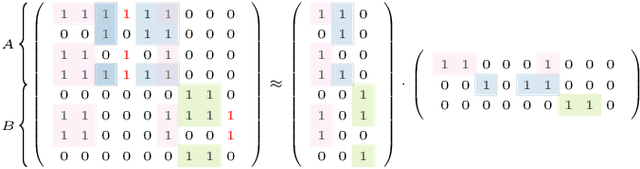
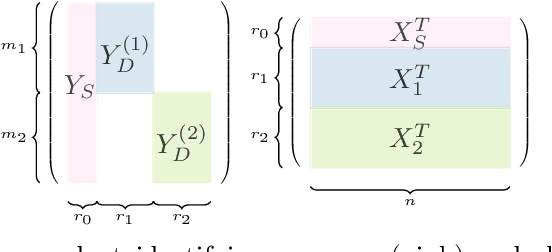
Given labeled data represented by a binary matrix, we consider the task to derive a Boolean matrix factorization which identifies commonalities and specifications among the classes. While existing works focus on rank-one factorizations which are either specific or common to the classes, we derive class-specific alterations from common factorizations as well. Therewith, we broaden the applicability of our new method to datasets whose class-dependencies have a more complex structure. On the basis of synthetic and real-world datasets, we show on the one hand that our method is able to filter structure which corresponds to our model assumption, and on the other hand that our model assumption is justified in real-world application. Our method is parameter-free.

The PRIMPing Routine -- Tiling through Proximal Alternating Linearized Minimization

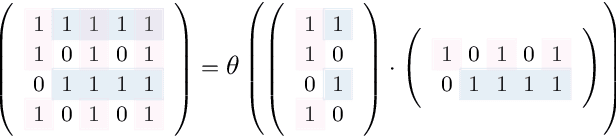
Mining and exploring databases should provide users with knowledge and new insights. Tiles of data strive to unveil true underlying structure and distinguish valuable information from various kinds of noise. We propose a novel Boolean matrix factorization algorithm to solve the tiling problem, based on recent results from optimization theory. In contrast to existing work, the new algorithm minimizes the description length of the resulting factorization. This approach is well known for model selection and data compression, but not for finding suitable factorizations via numerical optimization. We demonstrate the superior robustness of the new approach in the presence of several kinds of noise and types of underlying structure. Moreover, our general framework can work with any cost measure having a suitable real-valued relaxation. Thereby, no convexity assumptions have to be met. The experimental results on synthetic data and image data show that the new method identifies interpretable patterns which explain the data almost always better than the competing algorithms.