C-SALT: Mining Class-Specific ALTerations in Boolean Matrix Factorization
Paper and Code
Jun 17, 2019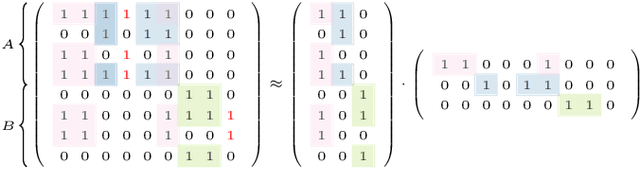

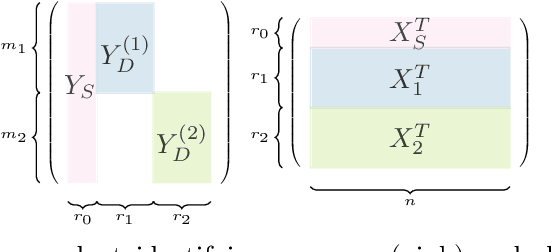

Given labeled data represented by a binary matrix, we consider the task to derive a Boolean matrix factorization which identifies commonalities and specifications among the classes. While existing works focus on rank-one factorizations which are either specific or common to the classes, we derive class-specific alterations from common factorizations as well. Therewith, we broaden the applicability of our new method to datasets whose class-dependencies have a more complex structure. On the basis of synthetic and real-world datasets, we show on the one hand that our method is able to filter structure which corresponds to our model assumption, and on the other hand that our model assumption is justified in real-world application. Our method is parameter-free.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge