The Trustworthy Pal: Controlling the False Discovery Rate in Boolean Matrix Factorization
Paper and Code
Jul 01, 2019
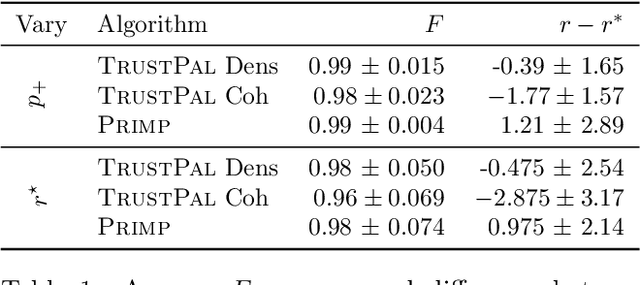

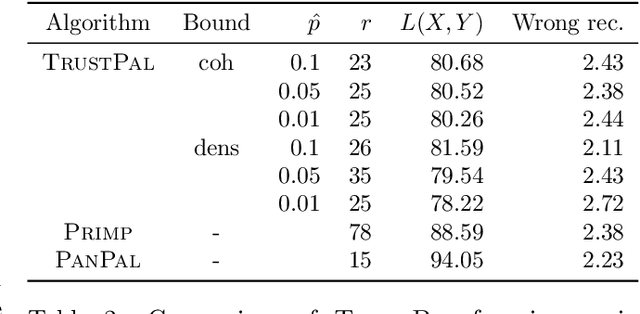
Boolean matrix factorization (BMF) is a popular and powerful technique for inferring knowledge from data. The mining result is the Boolean product of two matrices, approximating the input dataset. The Boolean product is a disjunction of rank-1 binary matrices, each describing a feature-relation, called pattern, for a group of samples. Yet, there are no guarantees that any of the returned patterns do not actually arise from noise, i.e., are false discoveries. In this paper, we propose and discuss the usage of the false discovery rate in the unsupervised BMF setting. We prove two bounds on the probability that a found pattern is constituted of random Bernoulli-distributed noise. Each bound exploits a specific property of the factorization which minimizes the approximation error---yielding new insights on the minimizers of Boolean matrix factorization. This leads to improved BMF algorithms by replacing heuristic rank selection techniques with a theoretically well-based approach. Our empirical demonstration shows that both bounds deliver excellent results in various practical settings.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge