Fast Inference of Tree Ensembles on ARM Devices

With the ongoing integration of Machine Learning models into everyday life, e.g. in the form of the Internet of Things (IoT), the evaluation of learned models becomes more and more an important issue. Tree ensembles are one of the best black-box classifiers available and routinely outperform more complex classifiers. While the fast application of tree ensembles has already been studied in the literature for Intel CPUs, they have not yet been studied in the context of ARM CPUs which are more dominant for IoT applications. In this paper, we convert the popular QuickScorer algorithm and its siblings from Intel's AVX to ARM's NEON instruction set. Second, we extend our implementation from ranking models to classification models such as Random Forests. Third, we investigate the effects of using fixed-point quantization in Random Forests. Our study shows that a careful implementation of tree traversal on ARM CPUs leads to a speed-up of up to 9.4 compared to a reference implementation. Moreover, quantized models seem to outperform models using floating-point values in terms of speed in almost all cases, with a neglectable impact on the predictive performance of the model. Finally, our study highlights architectural differences between ARM and Intel CPUs and between different ARM devices that imply that the best implementation depends on both the specific forest as well as the specific device used for deployment.

Shrub Ensembles for Online Classification

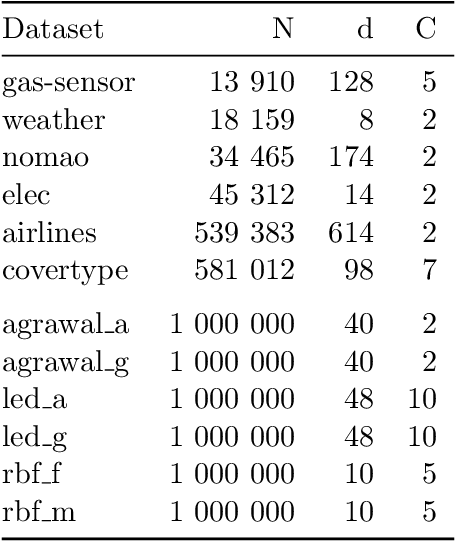
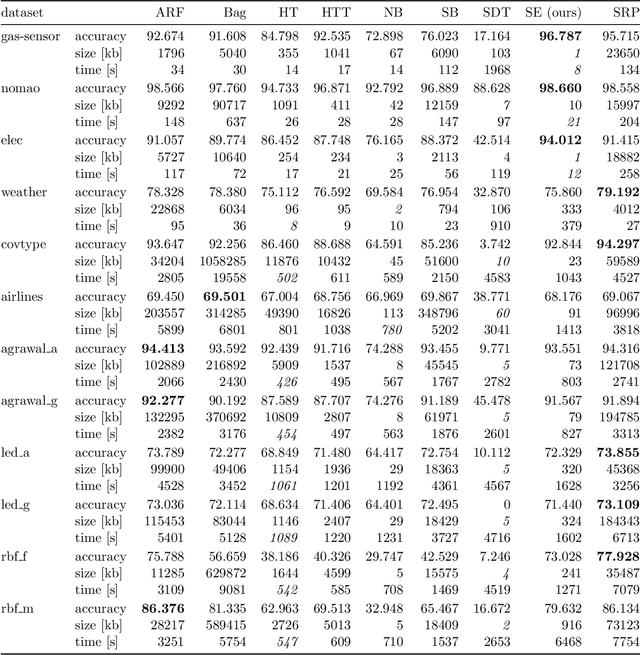
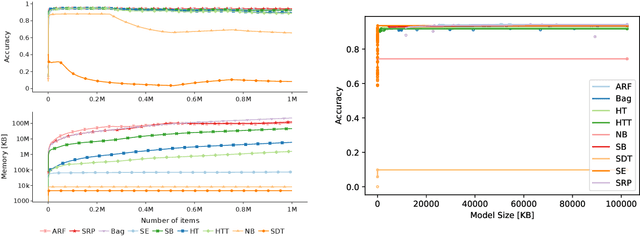
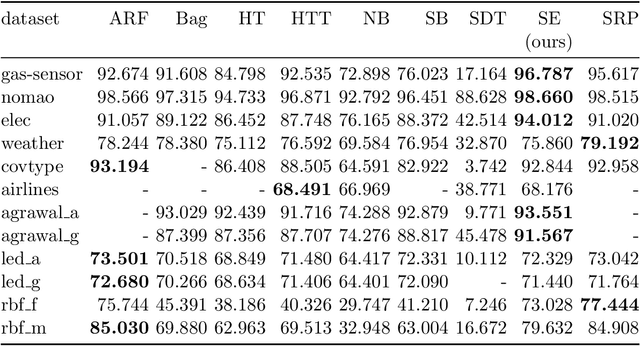
Online learning algorithms have become a ubiquitous tool in the machine learning toolbox and are frequently used in small, resource-constraint environments. Among the most successful online learning methods are Decision Tree (DT) ensembles. DT ensembles provide excellent performance while adapting to changes in the data, but they are not resource efficient. Incremental tree learners keep adding new nodes to the tree but never remove old ones increasing the memory consumption over time. Gradient-based tree learning, on the other hand, requires the computation of gradients over the entire tree which is costly for even moderately sized trees. In this paper, we propose a novel memory-efficient online classification ensemble called shrub ensembles for resource-constraint systems. Our algorithm trains small to medium-sized decision trees on small windows and uses stochastic proximal gradient descent to learn the ensemble weights of these `shrubs'. We provide a theoretical analysis of our algorithm and include an extensive discussion on the behavior of our approach in the online setting. In a series of 2~959 experiments on 12 different datasets, we compare our method against 8 state-of-the-art methods. Our Shrub Ensembles retain an excellent performance even when only little memory is available. We show that SE offers a better accuracy-memory trade-off in 7 of 12 cases, while having a statistically significant better performance than most other methods. Our implementation is available under https://github.com/sbuschjaeger/se-online .

There is no Double-Descent in Random Forests

Random Forests (RFs) are among the state-of-the-art in machine learning and offer excellent performance with nearly zero parameter tuning. Remarkably, RFs seem to be impervious to overfitting even though their basic building blocks are well-known to overfit. Recently, a broadly received study argued that a RF exhibits a so-called double-descent curve: First, the model overfits the data in a u-shaped curve and then, once a certain model complexity is reached, it suddenly improves its performance again. In this paper, we challenge the notion that model capacity is the correct tool to explain the success of RF and argue that the algorithm which trains the model plays a more important role than previously thought. We show that a RF does not exhibit a double-descent curve but rather has a single descent. Hence, it does not overfit in the classic sense. We further present a RF variation that also does not overfit although its decision boundary approximates that of an overfitted DT. Similar, we show that a DT which approximates the decision boundary of a RF will still overfit. Last, we study the diversity of an ensemble as a tool the estimate its performance. To do so, we introduce Negative Correlation Forest (NCForest) which allows for precise control over the diversity in the ensemble. We show, that the diversity and the bias indeed have a crucial impact on the performance of the RF. Having too low diversity collapses the performance of the RF into a a single tree, whereas having too much diversity means that most trees do not produce correct outputs anymore. However, in-between these two extremes we find a large range of different trade-offs with all roughly equal performance. Hence, the specific trade-off between bias and diversity does not matter as long as the algorithm reaches this good trade-off regime.

Improving the Accuracy-Memory Trade-Off of Random Forests Via Leaf-Refinement

Random Forests (RF) are among the state-of-the-art in many machine learning applications. With the ongoing integration of ML models into everyday life, the deployment and continuous application of models becomes more and more an important issue. Hence, small models which offer good predictive performance but use small amounts of memory are required. Ensemble pruning is a standard technique to remove unnecessary classifiers from an ensemble to reduce the overall resource consumption and sometimes even improve the performance of the original ensemble. In this paper, we revisit ensemble pruning in the context of `modernly' trained Random Forests where trees are very large. We show that the improvement effects of pruning diminishes for ensembles of large trees but that pruning has an overall better accuracy-memory trade-off than RF. However, pruning does not offer fine-grained control over this trade-off because it removes entire trees from the ensemble. To further improve the accuracy-memory trade-off we present a simple, yet surprisingly effective algorithm that refines the predictions in the leaf nodes in the forest via stochastic gradient descent. We evaluate our method against 7 state-of-the-art pruning methods and show that our method outperforms the other methods on 11 of 16 datasets with a statistically significant better accuracy-memory trade-off compared to most methods. We conclude our experimental evaluation with a case study showing that our method can be applied in a real-world setting.

Providing Meaningful Data Summarizations Using Examplar-based Clustering in Industry 4.0

Data summarizations are a valuable tool to derive knowledge from large data streams and have proven their usefulness in a great number of applications. Summaries can be found by optimizing submodular functions. These functions map subsets of data to real values, which indicate their "representativeness" and which should be maximized to find a diverse summary of the underlying data. In this paper, we studied Exemplar-based clustering as a submodular function and provide a GPU algorithm to cope with its high computational complexity. We show, that our GPU implementation provides speedups of up to 72x using single-precision and up to 452x using half-precision computation compared to conventional CPU algorithms. We also show, that the GPU algorithm not only provides remarkable runtime benefits with workstation-grade GPUs but also with low-power embedded computation units for which speedups of up to 35x are possible. Furthermore, we apply our algorithm to real-world data from injection molding manufacturing processes and discuss how found summaries help with steering this specific process to cut costs and reduce the manufacturing of bad parts. Beyond pure speedup considerations, we show, that our approach can provide summaries within reasonable time frames for this kind of industrial, real-world data.

Bit Error Tolerance Metrics for Binarized Neural Networks

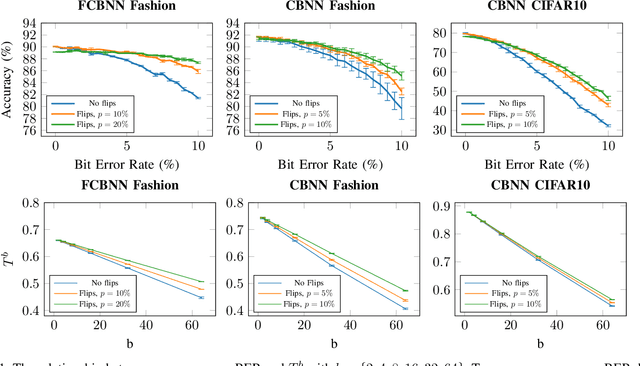
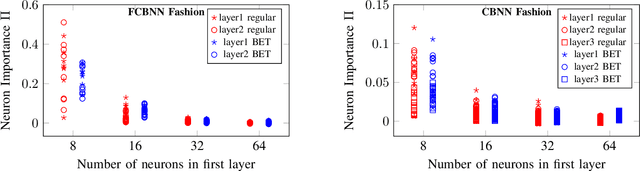
To reduce the resource demand of neural network (NN) inference systems, it has been proposed to use approximate memory, in which the supply voltage and the timing parameters are tuned trading accuracy with energy consumption and performance. Tuning these parameters aggressively leads to bit errors, which can be tolerated by NNs when bit flips are injected during training. However, bit flip training, which is the state of the art for achieving bit error tolerance, does not scale well; it leads to massive overheads and cannot be applied for high bit error rates (BERs). Alternative methods to achieve bit error tolerance in NNs are needed, but the underlying principles behind the bit error tolerance of NNs have not been reported yet. With this lack of understanding, further progress in the research on NN bit error tolerance will be restrained. In this study, our objective is to investigate the internal changes in the NNs that bit flip training causes, with a focus on binarized NNs (BNNs). To this end, we quantify the properties of bit error tolerant BNNs with two metrics. First, we propose a neuron-level bit error tolerance metric, which calculates the margin between the pre-activation values and batch normalization thresholds. Secondly, to capture the effects of bit error tolerance on the interplay of neurons, we propose an inter-neuron bit error tolerance metric, which measures the importance of each neuron and computes the variance over all importance values. Our experimental results support that these two metrics are strongly related to bit error tolerance.

GPU-Accelerated Optimizer-Aware Evaluation of Submodular Exemplar Clustering

The optimization of submodular functions constitutes a viable way to perform clustering. Strong approximation guarantees and feasible optimization w.r.t. streaming data make this clustering approach favorable. Technically, submodular functions map subsets of data to real values, which indicate how "representative" a specific subset is. Optimal sets might then be used to partition the data space and to infer clusters. Exemplar-based clustering is one of the possible submodular functions, but suffers from high computational complexity. However, for practical applications, the particular real-time or wall-clock run-time is decisive. In this work, we present a novel way to evaluate this particular function on GPUs, which keeps the necessities of optimizers in mind and reduces wall-clock run-time. To discuss our GPU algorithm, we investigated both the impact of different run-time critical problem properties, like data dimensionality and the number of data points in a subset, and the influence of required floating-point precision. In reproducible experiments, our GPU algorithm was able to achieve competitive speedups of up to 72x depending on whether multi-threaded computation on CPUs was used for comparison and the type of floating-point precision required. Half-precision GPU computation led to large speedups of up to 452x compared to single-precision, single-thread CPU computations.

Generalized Negative Correlation Learning for Deep Ensembling

Ensemble algorithms offer state of the art performance in many machine learning applications. A common explanation for their excellent performance is due to the bias-variance decomposition of the mean squared error which shows that the algorithm's error can be decomposed into its bias and variance. Both quantities are often opposed to each other and ensembles offer an effective way to manage them as they reduce the variance through a diverse set of base learners while keeping the bias low at the same time. Even though there have been numerous works on decomposing other loss functions, the exact mathematical connection is rarely exploited explicitly for ensembling, but merely used as a guiding principle. In this paper, we formulate a generalized bias-variance decomposition for arbitrary twice differentiable loss functions and study it in the context of Deep Learning. We use this decomposition to derive a Generalized Negative Correlation Learning (GNCL) algorithm which offers explicit control over the ensemble's diversity and smoothly interpolates between the two extremes of independent training and the joint training of the ensemble. We show how GNCL encapsulates many previous works and discuss under which circumstances training of an ensemble of Neural Networks might fail and what ensembling method should be favored depending on the choice of the individual networks.

Very Fast Streaming Submodular Function Maximization

Data summarization has become a valuable tool in understanding even terabytes of data. Due to their compelling theoretical properties, submodular functions have been in the focus of summarization algorithms. These algorithms offer worst-case approximations guarantees to the expense of higher computation and memory requirements. However, many practical applications do not fall under this worst-case, but are usually much more well-behaved. In this paper, we propose a new submodular function maximization algorithm called ThreeSieves, which ignores the worst-case, but delivers a good solution in high probability. It selects the most informative items from a data-stream on the fly and maintains a provable performance on a fixed memory budget. In an extensive evaluation we compare our method against $5$ other methods with over $3895$ hyperparameter configurations. We show that our algorithm outperforms current state-of-the-art algorithms and, at the same time, uses fewer resources. Last, we highlight a real-world use-case of our algorithm for data summarization in gamma-ray astronomy. We make our code publicly available at https://github.com/sbuschjaeger/SubmodularStreamingMaximization