Kolmogorov-Arnold Network for Transistor Compact Modeling

Neural network (NN)-based transistor compact modeling has recently emerged as a transformative solution for accelerating device modeling and SPICE circuit simulations. However, conventional NN architectures, despite their widespread adoption in state-of-the-art methods, primarily function as black-box problem solvers. This lack of interpretability significantly limits their capacity to extract and convey meaningful insights into learned data patterns, posing a major barrier to their broader adoption in critical modeling tasks. This work introduces, for the first time, Kolmogorov-Arnold network (KAN) for the transistor - a groundbreaking NN architecture that seamlessly integrates interpretability with high precision in physics-based function modeling. We systematically evaluate the performance of KAN and Fourier KAN for FinFET compact modeling, benchmarking them against the golden industry-standard compact model and the widely used MLP architecture. Our results reveal that KAN and FKAN consistently achieve superior prediction accuracy for critical figures of merit, including gate current, drain charge, and source charge. Furthermore, we demonstrate and improve the unique ability of KAN to derive symbolic formulas from learned data patterns - a capability that not only enhances interpretability but also facilitates in-depth transistor analysis and optimization. This work highlights the transformative potential of KAN in bridging the gap between interpretability and precision in NN-driven transistor compact modeling. By providing a robust and transparent approach to transistor modeling, KAN represents a pivotal advancement for the semiconductor industry as it navigates the challenges of advanced technology scaling.

Bit Error Tolerance Metrics for Binarized Neural Networks

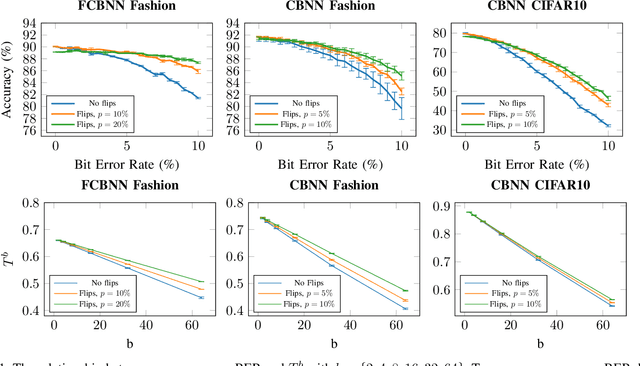
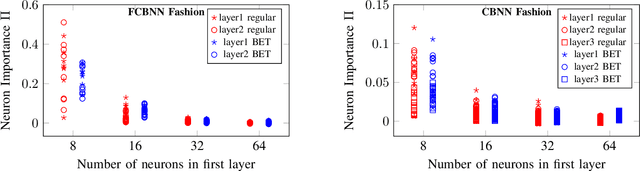
To reduce the resource demand of neural network (NN) inference systems, it has been proposed to use approximate memory, in which the supply voltage and the timing parameters are tuned trading accuracy with energy consumption and performance. Tuning these parameters aggressively leads to bit errors, which can be tolerated by NNs when bit flips are injected during training. However, bit flip training, which is the state of the art for achieving bit error tolerance, does not scale well; it leads to massive overheads and cannot be applied for high bit error rates (BERs). Alternative methods to achieve bit error tolerance in NNs are needed, but the underlying principles behind the bit error tolerance of NNs have not been reported yet. With this lack of understanding, further progress in the research on NN bit error tolerance will be restrained. In this study, our objective is to investigate the internal changes in the NNs that bit flip training causes, with a focus on binarized NNs (BNNs). To this end, we quantify the properties of bit error tolerant BNNs with two metrics. First, we propose a neuron-level bit error tolerance metric, which calculates the margin between the pre-activation values and batch normalization thresholds. Secondly, to capture the effects of bit error tolerance on the interplay of neurons, we propose an inter-neuron bit error tolerance metric, which measures the importance of each neuron and computes the variance over all importance values. Our experimental results support that these two metrics are strongly related to bit error tolerance.

Towards Explainable Bit Error Tolerance of Resistive RAM-Based Binarized Neural Networks

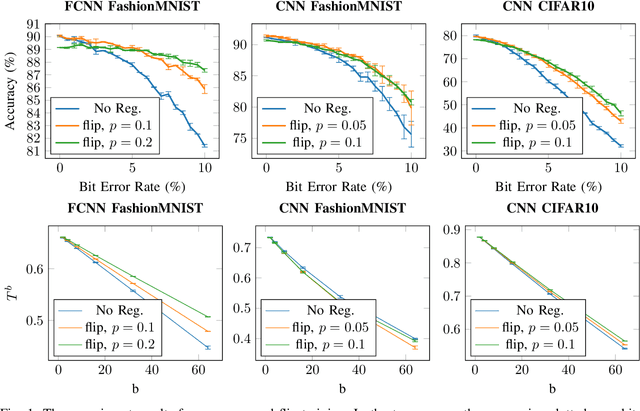
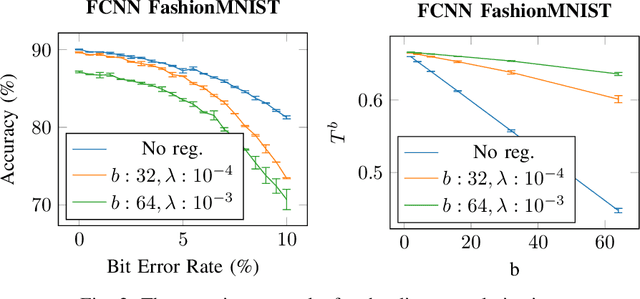
Non-volatile memory, such as resistive RAM (RRAM), is an emerging energy-efficient storage, especially for low-power machine learning models on the edge. It is reported, however, that the bit error rate of RRAMs can be up to 3.3% in the ultra low-power setting, which might be crucial for many use cases. Binary neural networks (BNNs), a resource efficient variant of neural networks (NNs), can tolerate a certain percentage of errors without a loss in accuracy and demand lower resources in computation and storage. The bit error tolerance (BET) in BNNs can be achieved by flipping the weight signs during training, as proposed by Hirtzlin et al., but their method has a significant drawback, especially for fully connected neural networks (FCNN): The FCNNs overfit to the error rate used in training, which leads to low accuracy under lower error rates. In addition, the underlying principles of BET are not investigated. In this work, we improve the training for BET of BNNs and aim to explain this property. We propose straight-through gradient approximation to improve the weight-sign-flip training, by which BNNs adapt less to the bit error rates. To explain the achieved robustness, we define a metric that aims to measure BET without fault injection. We evaluate the metric and find that it correlates with accuracy over error rate for all FCNNs tested. Finally, we explore the influence of a novel regularizer that optimizes with respect to this metric, with the aim of providing a configurable trade-off in accuracy and BET.