Bridging the Gap between ROS~2 and Classical Real-Time Scheduling for Periodic Tasks

The Robot Operating System 2 (ROS~2) is a widely used middleware that provides software libraries and tools for developing robotic systems. In these systems, tasks are scheduled by ROS~2 executors. Since the scheduling behavior of the default ROS~2 executor is inherently different from classical real-time scheduling theory, dedicated analyses or alternative executors, requiring substantial changes to ROS~2, have been required. In 2023, the events executor, which features an events queue and allows the possibility to make scheduling decisions immediately after a job completes, was introduced into ROS~2. In this paper, we show that, with only minor modifications of the events executor, a large body of research results from classical real-time scheduling theory becomes applicable. Hence, this enables analytical bounds on the worst-case response time and the end-to-end latency, outperforming bounds for the default ROS 2 executor in many scenarios. Our solution is easy to integrate into existing ROS 2 systems since it requires only minor backend modifications of the events executor, which is natively included in ROS 2. The evaluation results show that our ROS~2 events executor with minor modifications can have significant improvement in terms of dropped jobs, worst-case response time, end-to-end latency, and performance compared to the default ROS~2 executor.

Universal Approximation Theorems of Fully Connected Binarized Neural Networks

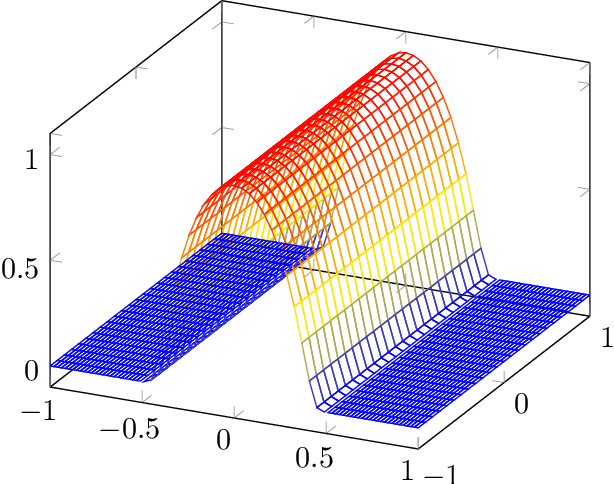
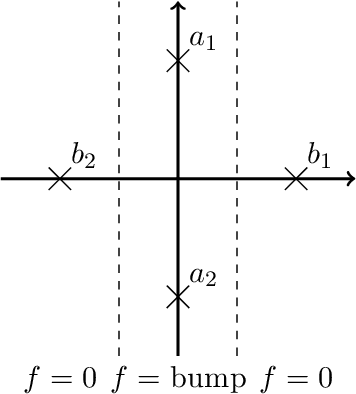
Neural networks (NNs) are known for their high predictive accuracy in complex learning problems. Beside practical advantages, NNs also indicate favourable theoretical properties such as universal approximation (UA) theorems. Binarized Neural Networks (BNNs) significantly reduce time and memory demands by restricting the weight and activation domains to two values. Despite the practical advantages, theoretical guarantees based on UA theorems of BNNs are rather sparse in the literature. We close this gap by providing UA theorems for fully connected BNNs under the following scenarios: (1) for binarized inputs, UA can be constructively achieved under one hidden layer; (2) for inputs with real numbers, UA can not be achieved under one hidden layer but can be constructively achieved under two hidden layers for Lipschitz-continuous functions. Our results indicate that fully connected BNNs can approximate functions universally, under certain conditions.

Bit Error Tolerance Metrics for Binarized Neural Networks

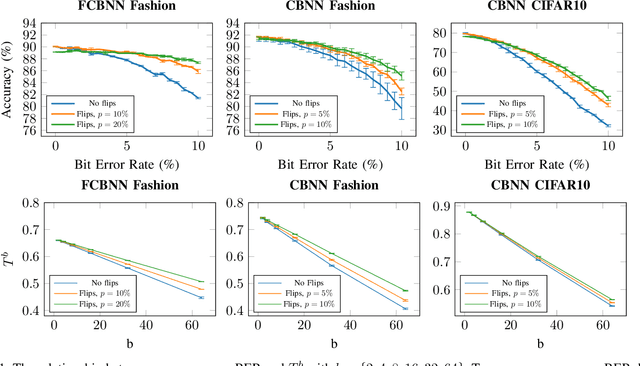
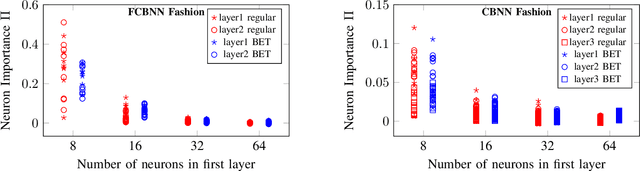
To reduce the resource demand of neural network (NN) inference systems, it has been proposed to use approximate memory, in which the supply voltage and the timing parameters are tuned trading accuracy with energy consumption and performance. Tuning these parameters aggressively leads to bit errors, which can be tolerated by NNs when bit flips are injected during training. However, bit flip training, which is the state of the art for achieving bit error tolerance, does not scale well; it leads to massive overheads and cannot be applied for high bit error rates (BERs). Alternative methods to achieve bit error tolerance in NNs are needed, but the underlying principles behind the bit error tolerance of NNs have not been reported yet. With this lack of understanding, further progress in the research on NN bit error tolerance will be restrained. In this study, our objective is to investigate the internal changes in the NNs that bit flip training causes, with a focus on binarized NNs (BNNs). To this end, we quantify the properties of bit error tolerant BNNs with two metrics. First, we propose a neuron-level bit error tolerance metric, which calculates the margin between the pre-activation values and batch normalization thresholds. Secondly, to capture the effects of bit error tolerance on the interplay of neurons, we propose an inter-neuron bit error tolerance metric, which measures the importance of each neuron and computes the variance over all importance values. Our experimental results support that these two metrics are strongly related to bit error tolerance.

Towards Explainable Bit Error Tolerance of Resistive RAM-Based Binarized Neural Networks

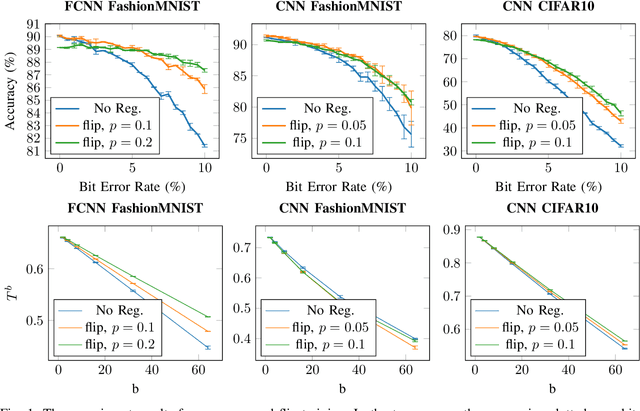
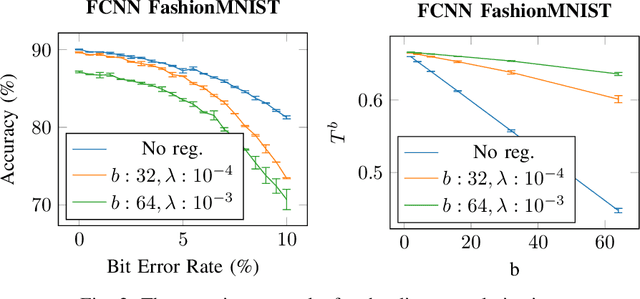
Non-volatile memory, such as resistive RAM (RRAM), is an emerging energy-efficient storage, especially for low-power machine learning models on the edge. It is reported, however, that the bit error rate of RRAMs can be up to 3.3% in the ultra low-power setting, which might be crucial for many use cases. Binary neural networks (BNNs), a resource efficient variant of neural networks (NNs), can tolerate a certain percentage of errors without a loss in accuracy and demand lower resources in computation and storage. The bit error tolerance (BET) in BNNs can be achieved by flipping the weight signs during training, as proposed by Hirtzlin et al., but their method has a significant drawback, especially for fully connected neural networks (FCNN): The FCNNs overfit to the error rate used in training, which leads to low accuracy under lower error rates. In addition, the underlying principles of BET are not investigated. In this work, we improve the training for BET of BNNs and aim to explain this property. We propose straight-through gradient approximation to improve the weight-sign-flip training, by which BNNs adapt less to the bit error rates. To explain the achieved robustness, we define a metric that aims to measure BET without fault injection. We evaluate the metric and find that it correlates with accuracy over error rate for all FCNNs tested. Finally, we explore the influence of a novel regularizer that optimizes with respect to this metric, with the aim of providing a configurable trade-off in accuracy and BET.