On the Relation between Prediction and Imputation Accuracy under Missing Covariates

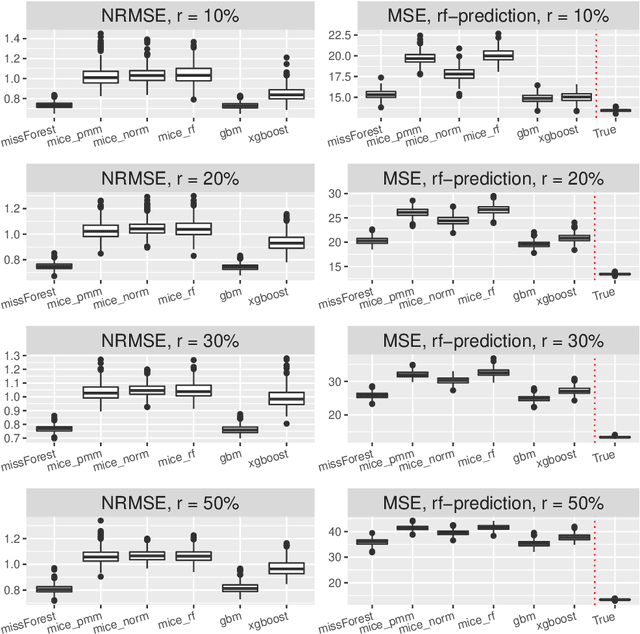
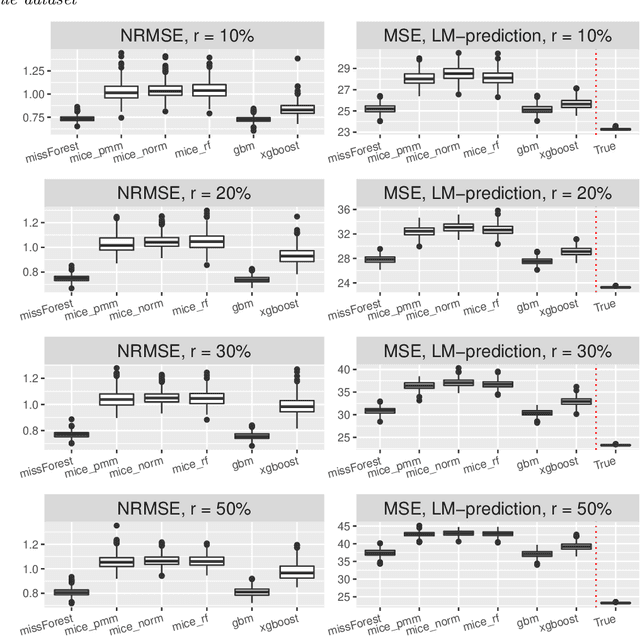
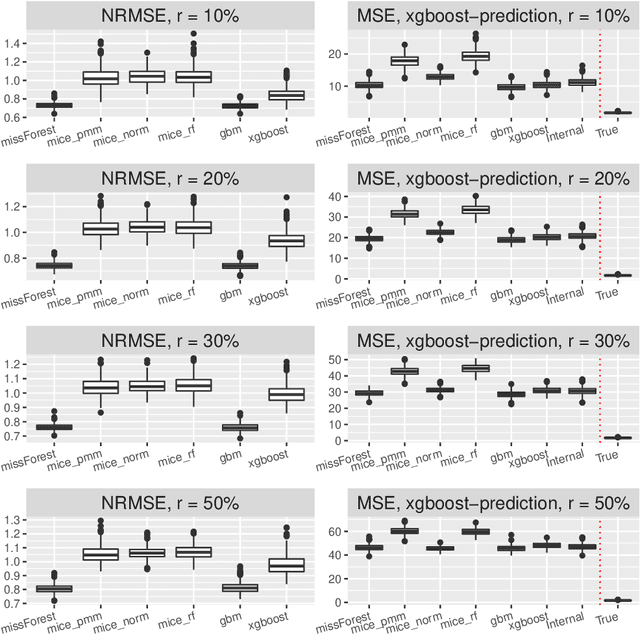
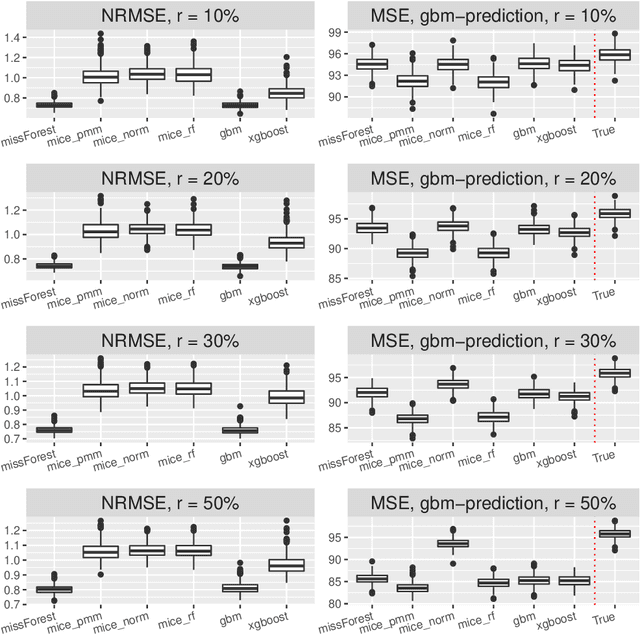
Missing covariates in regression or classification problems can prohibit the direct use of advanced tools for further analysis. Recent research has realized an increasing trend towards the usage of modern Machine Learning algorithms for imputation. It originates from their capability of showing favourable prediction accuracy in different learning problems. In this work, we analyze through simulation the interaction between imputation accuracy and prediction accuracy in regression learning problems with missing covariates when Machine Learning based methods for both, imputation and prediction are used. In addition, we explore imputation performance when using statistical inference procedures in prediction settings, such as coverage rates of (valid) prediction intervals. Our analysis is based on empirical datasets provided by the UCI Machine Learning repository and an extensive simulation study.

Interpretable Machines: Constructing Valid Prediction Intervals with Random Forests

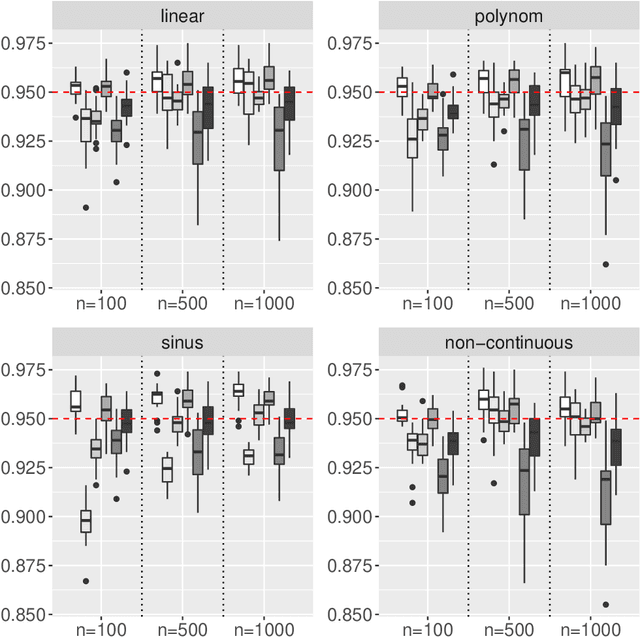
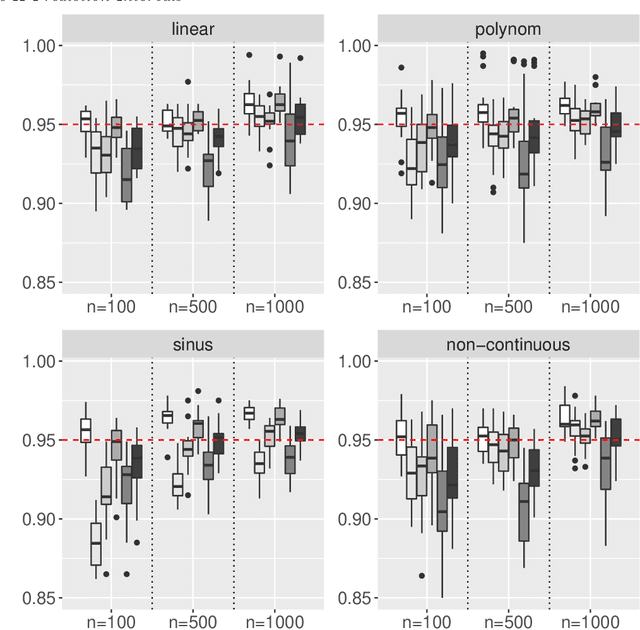
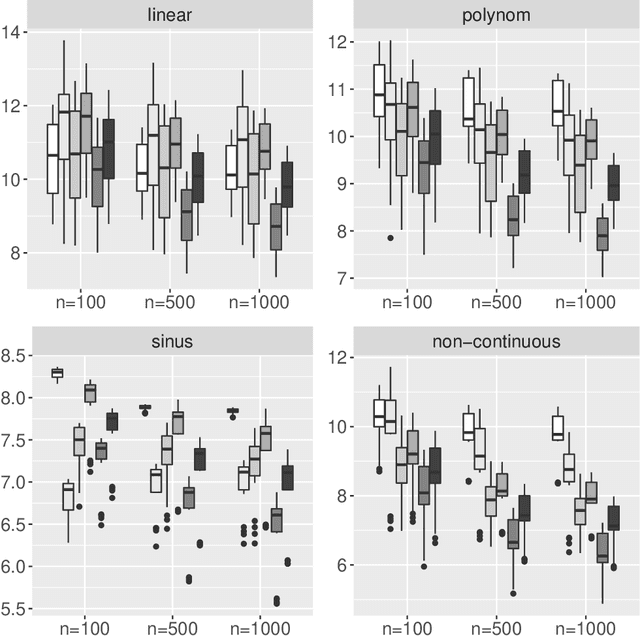
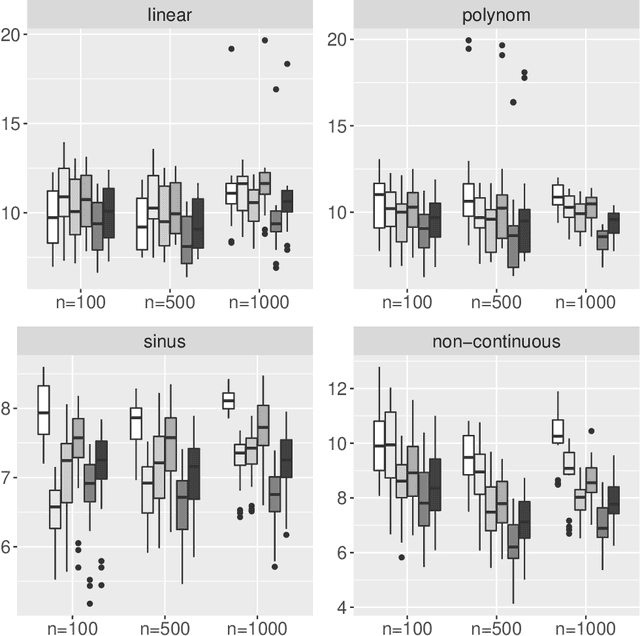
An important issue when using Machine Learning algorithms in recent research is the lack of interpretability. Although these algorithms provide accurate point predictions for various learning problems, uncertainty estimates connected with point predictions are rather sparse. A contribution to this gap for the Random Forest Regression Learner is presented here. Based on its Out-of-Bag procedure, several parametric and non-parametric prediction intervals are provided for Random Forest point predictions and theoretical guarantees for its correct coverage probability is delivered. In a second part, a thorough investigation through Monte-Carlo simulation is conducted evaluating the performance of the proposed methods from three aspects: (i) Analyzing the correct coverage rate of the proposed prediction intervals, (ii) Inspecting interval width and (iii) Verifying the competitiveness of the proposed intervals with existing methods. The simulation yields that the proposed prediction intervals are robust towards non-normal residual distributions and are competitive by providing correct coverage rates and comparably narrow interval lengths, even for comparably small samples.

Universal Approximation Theorems of Fully Connected Binarized Neural Networks

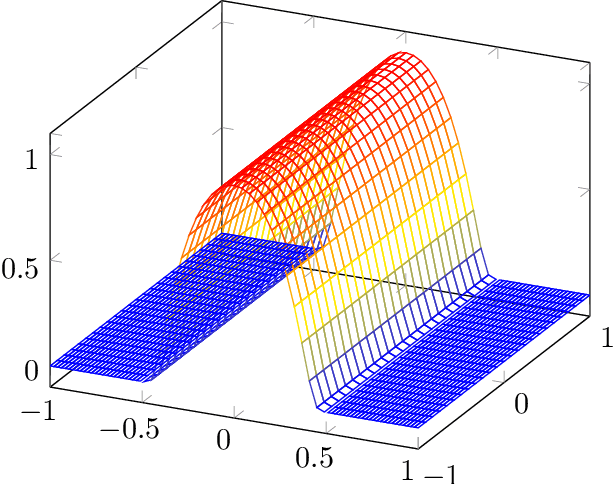
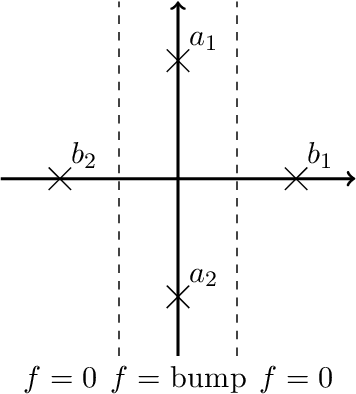
Neural networks (NNs) are known for their high predictive accuracy in complex learning problems. Beside practical advantages, NNs also indicate favourable theoretical properties such as universal approximation (UA) theorems. Binarized Neural Networks (BNNs) significantly reduce time and memory demands by restricting the weight and activation domains to two values. Despite the practical advantages, theoretical guarantees based on UA theorems of BNNs are rather sparse in the literature. We close this gap by providing UA theorems for fully connected BNNs under the following scenarios: (1) for binarized inputs, UA can be constructively achieved under one hidden layer; (2) for inputs with real numbers, UA can not be achieved under one hidden layer but can be constructively achieved under two hidden layers for Lipschitz-continuous functions. Our results indicate that fully connected BNNs can approximate functions universally, under certain conditions.

Asymptotic Unbiasedness of the Permutation Importance Measure in Random Forest Models

Variable selection in sparse regression models is an important task as applications ranging from biomedical research to econometrics have shown. Especially for higher dimensional regression problems, for which the link function between response and covariates cannot be directly detected, the selection of informative variables is challenging. Under these circumstances, the Random Forest method is a helpful tool to predict new outcomes while delivering measures for variable selection. One common approach is the usage of the permutation importance. Due to its intuitive idea and flexible usage, it is important to explore circumstances, for which the permutation importance based on Random Forest correctly indicates informative covariates. Regarding the latter, we deliver theoretical guarantees for the validity of the permutation importance measure under specific assumptions and prove its (asymptotic) unbiasedness. An extensive simulation study verifies our findings.

Who wins the Miss Contest for Imputation Methods? Our Vote for Miss BooPF

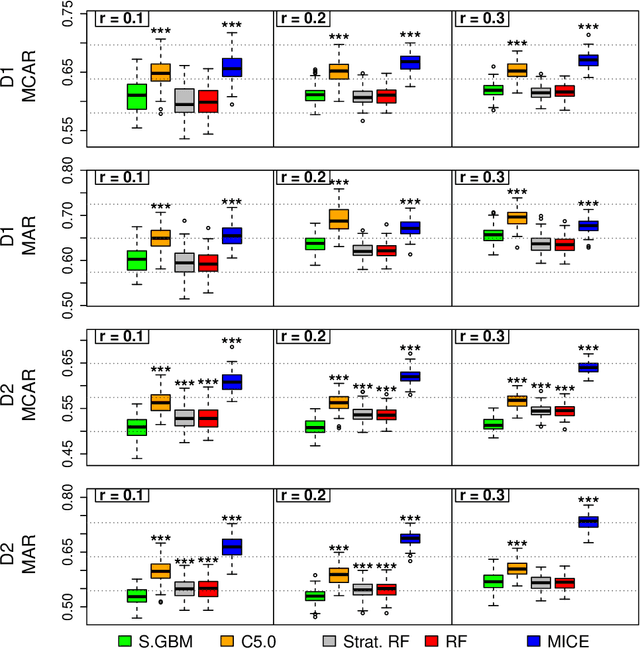
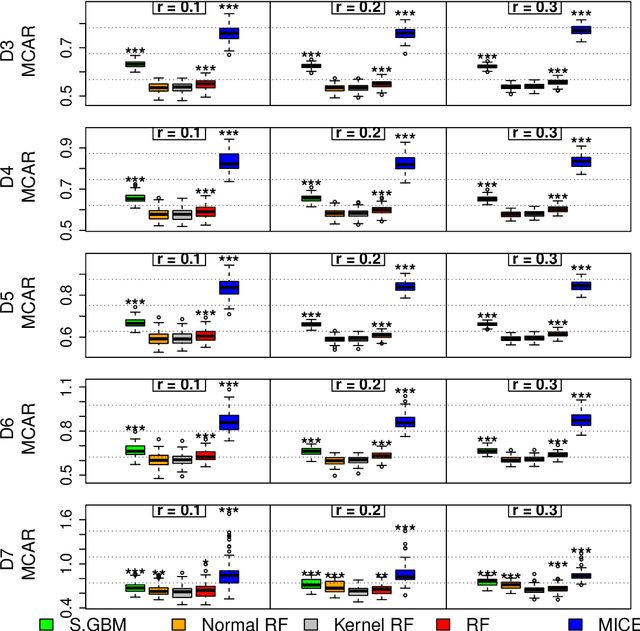
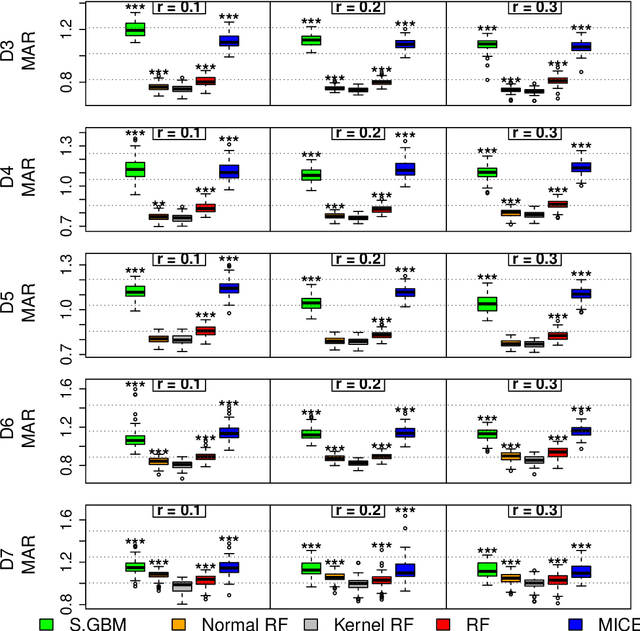
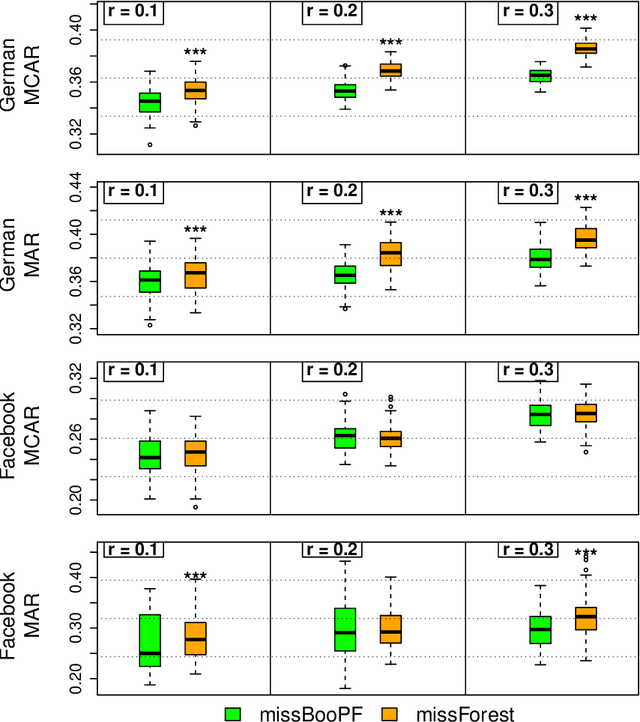
Missing data is an expected issue when large amounts of data is collected, and several imputation techniques have been proposed to tackle this problem. Beneath classical approaches such as MICE, the application of Machine Learning techniques is tempting. Here, the recently proposed missForest imputation method has shown high imputation accuracy under the Missing (Completely) at Random scheme with various missing rates. In its core, it is based on a random forest for classification and regression, respectively. In this paper we study whether this approach can even be enhanced by other methods such as the stochastic gradient tree boosting method, the C5.0 algorithm or modified random forest procedures. In particular, other resampling strategies within the random forest protocol are suggested. In an extensive simulation study, we analyze their performances for continuous, categorical as well as mixed-type data. Therein, MissBooPF, a combination of the stochastic gradient tree boosting method together with the parametrically bootstrapped random forest method, appeared to be promising. Finally, an empirical analysis focusing on credit information and Facebook data is conducted.