Beyond Discriminant Patterns: On the Robustness of Decision Rule Ensembles
Paper and Code
Sep 21, 2021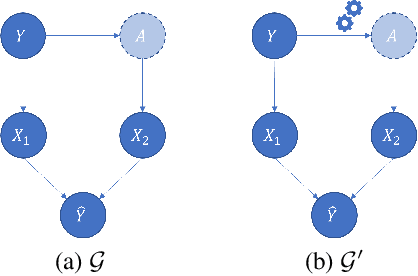
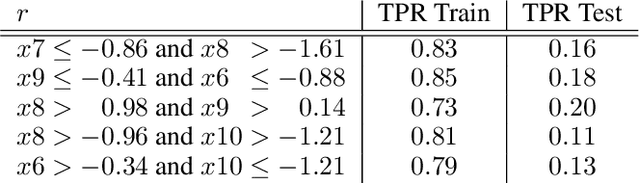

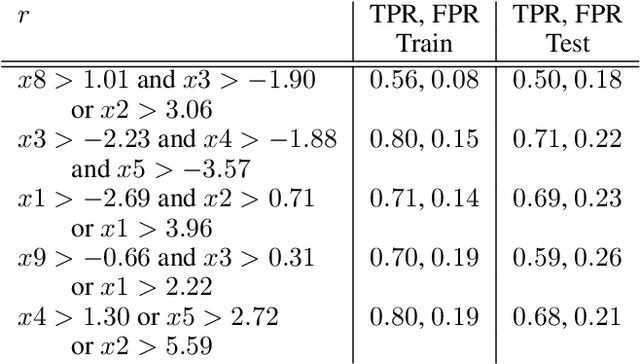
Local decision rules are commonly understood to be more explainable, due to the local nature of the patterns involved. With numerical optimization methods such as gradient boosting, ensembles of local decision rules can gain good predictive performance on data involving global structure. Meanwhile, machine learning models are being increasingly used to solve problems in high-stake domains including healthcare and finance. Here, there is an emerging consensus regarding the need for practitioners to understand whether and how those models could perform robustly in the deployment environments, in the presence of distributional shifts. Past research on local decision rules has focused mainly on maximizing discriminant patterns, without due consideration of robustness against distributional shifts. In order to fill this gap, we propose a new method to learn and ensemble local decision rules, that are robust both in the training and deployment environments. Specifically, we propose to leverage causal knowledge by regarding the distributional shifts in subpopulations and deployment environments as the results of interventions on the underlying system. We propose two regularization terms based on causal knowledge to search for optimal and stable rules. Experiments on both synthetic and benchmark datasets show that our method is effective and robust against distributional shifts in multiple environments.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge