An Image Segmentation Model with Transformed Total Variation

Based on transformed $\ell_1$ regularization, transformed total variation (TTV) has robust image recovery that is competitive with other nonconvex total variation (TV) regularizers, such as TV$^p$, $0<p<1$. Inspired by its performance, we propose a TTV-regularized Mumford--Shah model with fuzzy membership function for image segmentation. To solve it, we design an alternating direction method of multipliers (ADMM) algorithm that utilizes the transformed $\ell_1$ proximal operator. Numerical experiments demonstrate that using TTV is more effective than classical TV and other nonconvex TV variants in image segmentation.

A Proximal Algorithm for Network Slimming

As a popular channel pruning method for convolutional neural networks (CNNs), network slimming (NS) has a three-stage process: (1) it trains a CNN with $\ell_1$ regularization applied to the scaling factors of the batch normalization layers; (2) it removes channels whose scaling factors are below a chosen threshold; and (3) it retrains the pruned model to recover the original accuracy. This time-consuming, three-step process is a result of using subgradient descent to train CNNs. Because subgradient descent does not exactly train CNNs towards sparse, accurate structures, the latter two steps are necessary. Moreover, subgradient descent does not have any convergence guarantee. Therefore, we develop an alternative algorithm called proximal NS. Our proposed algorithm trains CNNs towards sparse, accurate structures, so identifying a scaling factor threshold is unnecessary and fine tuning the pruned CNNs is optional. Using Kurdyka-{\L}ojasiewicz assumptions, we establish global convergence of proximal NS. Lastly, we validate the efficacy of the proposed algorithm on VGGNet, DenseNet and ResNet on CIFAR 10/100. Our experiments demonstrate that after one round of training, proximal NS yields a CNN with competitive accuracy and compression.

Weighted Anisotropic-Isotropic Total Variation for Poisson Denoising

Poisson noise commonly occurs in images captured by photon-limited imaging systems such as in astronomy and medicine. As the distribution of Poisson noise depends on the pixel intensity value, noise levels vary from pixels to pixels. Hence, denoising a Poisson-corrupted image while preserving important details can be challenging. In this paper, we propose a Poisson denoising model by incorporating the weighted anisotropic-isotropic total variation (AITV) as a regularization. We then develop an alternating direction method of multipliers with a combination of a proximal operator for an efficient implementation. Lastly, numerical experiments demonstrate that our algorithm outperforms other Poisson denoising methods in terms of image quality and computational efficiency.

Efficient Image Segmentation Framework with Difference of Anisotropic and Isotropic Total Variation for Blur and Poisson Noise Removal

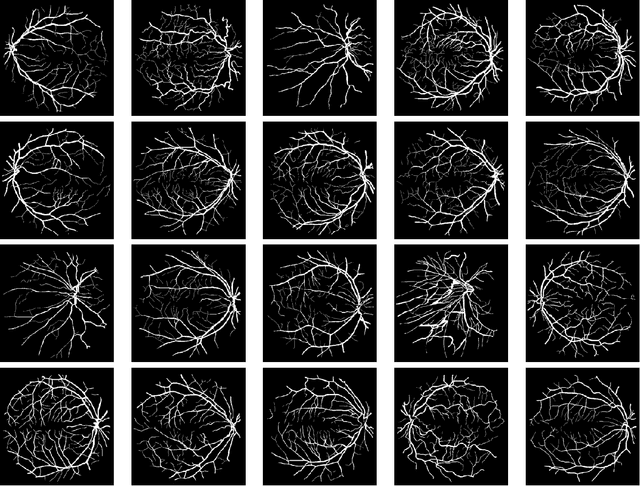
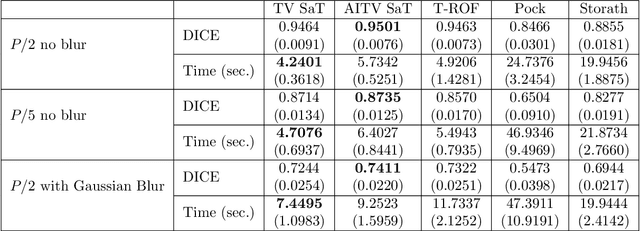
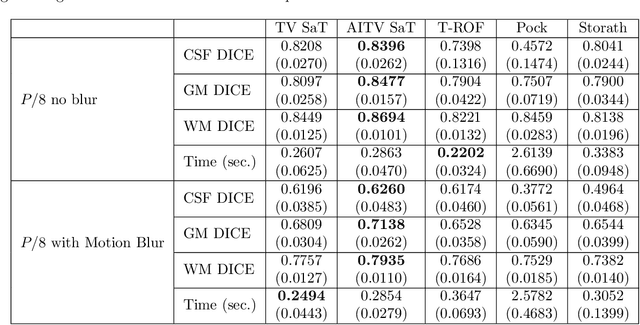
In this paper, we aim to segment an image degraded by blur and Poisson noise. We adopt a smoothing-and-thresholding (SaT) segmentation framework that finds a piecewise-smooth solution, followed by $k$-means clustering to segment the image. Specifically for the image smoothing step, we replace the least-squares fidelity for Gaussian noise in the Mumford-Shah model with a maximum posterior (MAP) term to deal with Poisson noise and we incorporate the weighted difference of anisotropic and isotropic total variation (AITV) as a regularization to promote the sparsity of image gradients. For such a nonconvex model, we develop a specific splitting scheme and utilize a proximal operator to apply the alternating direction method of multipliers (ADMM). Convergence analysis is provided to validate the efficacy of the ADMM scheme. Numerical experiments on various segmentation scenarios (grayscale/color and multiphase) showcase that our proposed method outperforms a number of segmentation methods, including the original SaT.

A Smoothing and Thresholding Image Segmentation Framework with Weighted Anisotropic-Isotropic Total Variation

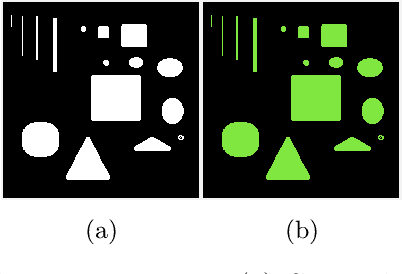
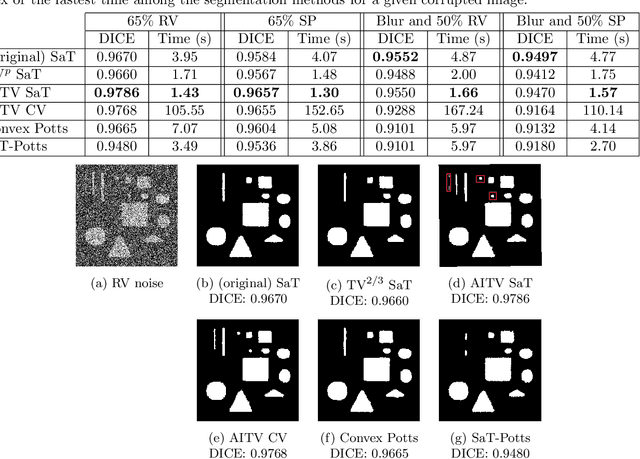
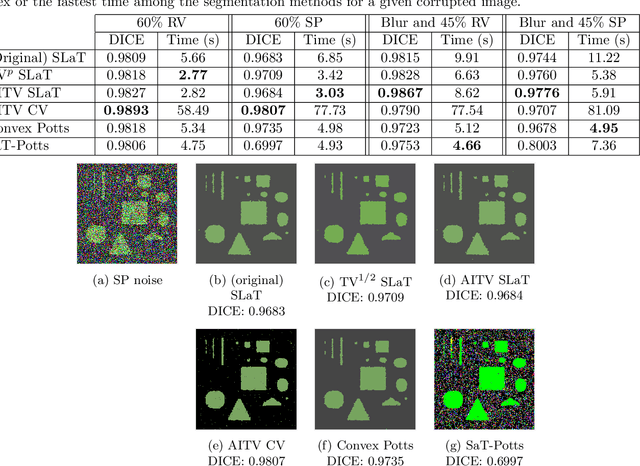
In this paper, we propose a multi-stage image segmentation framework that incorporates a weighted difference of anisotropic and isotropic total variation (AITV). The segmentation framework generally consists of two stages: smoothing and thresholding, thus referred to as SaT. In the first stage, a smoothed image is obtained by an AITV-regularized Mumford-Shah (MS) model, which can be solved efficiently by the alternating direction method of multipliers (ADMM) with a closed-form solution of a proximal operator of the $\ell_1 -\alpha \ell_2$ regularizer. Convergence of the ADMM algorithm is analyzed. In the second stage, we threshold the smoothed image by $k$-means clustering to obtain the final segmentation result. Numerical experiments demonstrate that the proposed segmentation framework is versatile for both grayscale and color images, efficient in producing high-quality segmentation results within a few seconds, and robust to input images that are corrupted with noise, blur, or both. We compare the AITV method with its original convex and nonconvex TV$^p (0<p<1)$ counterparts, showcasing the qualitative and quantitative advantages of our proposed method.

Nonconvex Regularization for Network Slimming:Compressing CNNs Even More

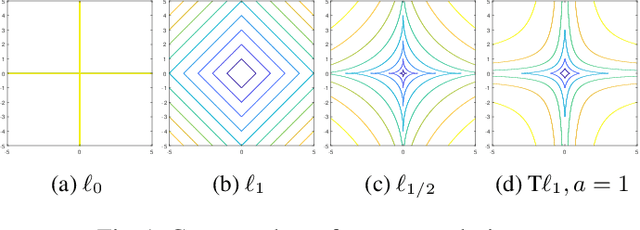
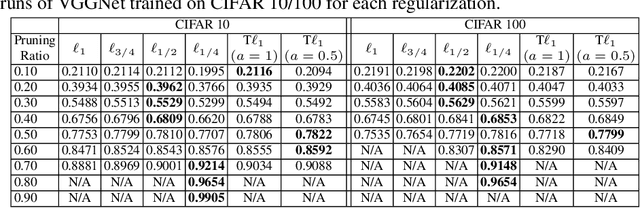
In the last decade, convolutional neural networks (CNNs) have evolved to become the dominant models for various computer vision tasks, but they cannot be deployed in low-memory devices due to its high memory requirement and computational cost. One popular, straightforward approach to compressing CNNs is network slimming, which imposes an $\ell_1$ penalty on the channel-associated scaling factors in the batch normalization layers during training. In this way, channels with low scaling factors are identified to be insignificant and are pruned in the models. In this paper, we propose replacing the $\ell_1$ penalty with the $\ell_p$ and transformed $\ell_1$ (T$\ell_1$) penalties since these nonconvex penalties outperformed $\ell_1$ in yielding sparser satisfactory solutions in various compressed sensing problems. In our numerical experiments, we demonstrate network slimming with $\ell_p$ and T$\ell_1$ penalties on VGGNet and Densenet trained on CIFAR 10/100. The results demonstrate that the nonconvex penalties compress CNNs better than $\ell_1$. In addition, T$\ell_1$ preserves the model accuracy after channel pruning, and $\ell_{1/2, 3/4}$ yield compressed models with similar accuracies as $\ell_1$ after retraining.

Clustering COVID-19 Lung Scans

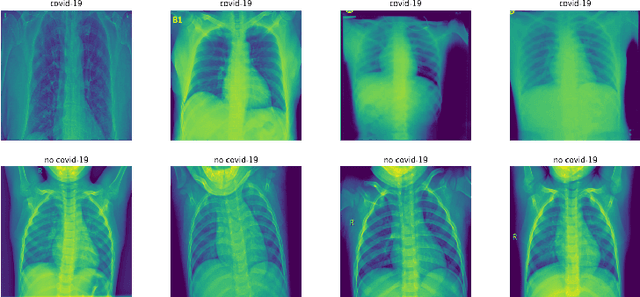
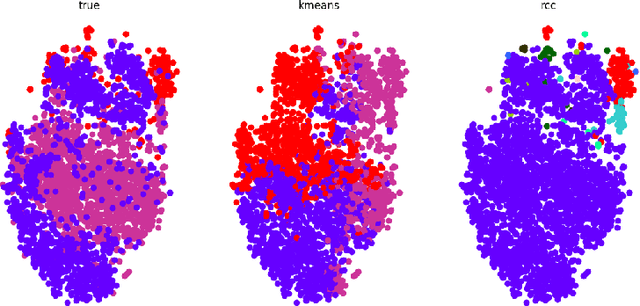
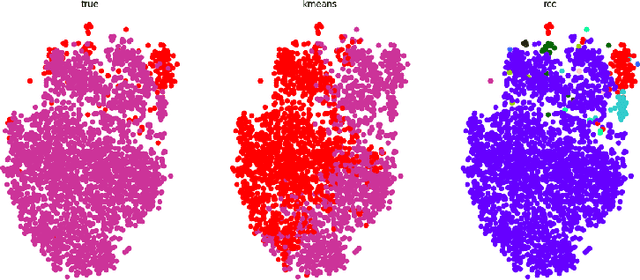
With the recent outbreak of COVID-19, creating a means to stop it's spread and eventually develop a vaccine are the most important and challenging tasks that the scientific community is facing right now. The first step towards these goals is to correctly identify a patient that is infected with the virus. Our group applied an unsupervised machine learning technique to identify COVID-19 cases. This is an important topic as COVID-19 is a novel disease currently being studied in detail and our methodology has the potential to reveal important differences between it and other viral pneumonia. This could then, in turn, enable doctors to more confidently help each patient. Our experiments utilize Principal Component Analysis (PCA), t-distributed Stochastic Neighbor Embedding (t-SNE), and the recently developed Robust Continuous Clustering algorithm (RCC). We display the performance of RCC in identifying COVID-19 patients and its ability to compete with other unsupervised algorithms, namely K-Means++ (KM++). Using a COVID-19 Radiography dataset, we found that RCC outperformed KM++; we used the Adjusted Mutual Information Score (AMI) in order to measure the effectiveness of both algorithms. The AMI for the two and three class cases of KM++ were 0.0250 and 0.054, respectively. In comparison, RCC scored 0.5044 in the two class case and 0.267 in the three class case, clearly showing RCC as the superior algorithm. This not only opens new possible applications of RCC, but it could potentially aid in the creation of a new tool for COVID-19 identification.

A Weighted Difference of Anisotropic and Isotropic Total Variation for Relaxed Mumford-Shah Color and Multiphase Image Segmentation

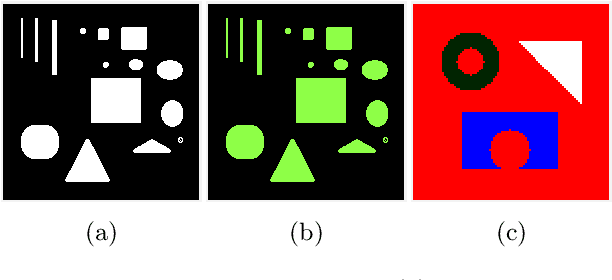
In a class of piecewise-constant image segmentation models, we incorporate a weighted difference of anisotropic and isotropic total variation (TV) to regularize the partition boundaries in an image. To deal with the weighted anisotropic-isotropic TV, we apply the difference-of-convex algorithm (DCA), where the subproblems can be minimized by the primal-dual hybrid gradient method (PDHG). As a result, we are able to design an alternating minimization algorithm to solve the proposed image segmentation models. The models and algorithms are further extended to segment color images and to perform multiphase segmentation. In the numerical experiments, we compare our proposed models with the Chan-Vese models that use either anisotropic or isotropic TV and the two-stage segmentation methods (denoising and then thresholding) on various images. The results demonstrate the effectiveness and robustness of incorporating weighted anisotropic-isotropic TV in image segmentation.

$\ell_0$ Regularized Structured Sparsity Convolutional Neural Networks

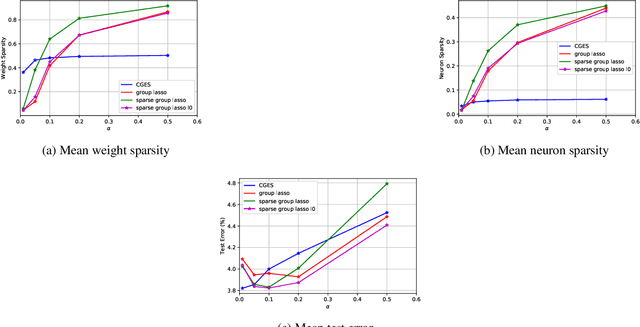
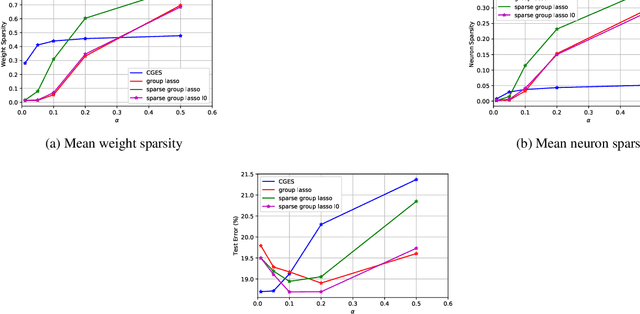
Deepening and widening convolutional neural networks (CNNs) significantly increases the number of trainable weight parameters by adding more convolutional layers and feature maps per layer, respectively. By imposing inter- and intra-group sparsity onto the weights of the layers during the training process, a compressed network can be obtained with accuracy comparable to a dense one. In this paper, we propose a new variant of sparse group lasso that blends the $\ell_0$ norm onto the individual weight parameters and the $\ell_{2,1}$ norm onto the output channels of a layer. To address the non-differentiability of the $\ell_0$ norm, we apply variable splitting resulting in an algorithm that consists of executing stochastic gradient descent followed by hard thresholding for each iteration. Numerical experiments are demonstrated on LeNet-5 and wide-residual-networks for MNIST and CIFAR 10/100, respectively. They showcase the effectiveness of our proposed method in attaining superior test accuracy with network sparsification on par with the current state of the art.