$\ell_0$ Regularized Structured Sparsity Convolutional Neural Networks
Paper and Code
Dec 17, 2019
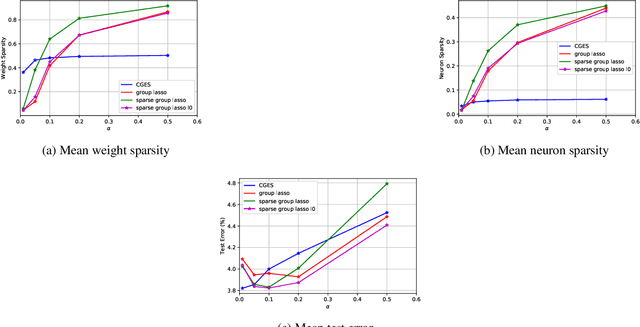
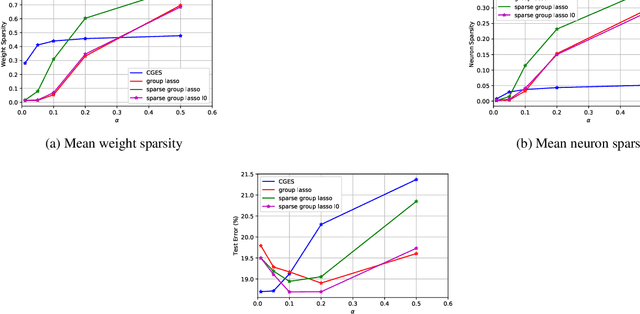
Deepening and widening convolutional neural networks (CNNs) significantly increases the number of trainable weight parameters by adding more convolutional layers and feature maps per layer, respectively. By imposing inter- and intra-group sparsity onto the weights of the layers during the training process, a compressed network can be obtained with accuracy comparable to a dense one. In this paper, we propose a new variant of sparse group lasso that blends the $\ell_0$ norm onto the individual weight parameters and the $\ell_{2,1}$ norm onto the output channels of a layer. To address the non-differentiability of the $\ell_0$ norm, we apply variable splitting resulting in an algorithm that consists of executing stochastic gradient descent followed by hard thresholding for each iteration. Numerical experiments are demonstrated on LeNet-5 and wide-residual-networks for MNIST and CIFAR 10/100, respectively. They showcase the effectiveness of our proposed method in attaining superior test accuracy with network sparsification on par with the current state of the art.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge