A Weighted Difference of Anisotropic and Isotropic Total Variation for Relaxed Mumford-Shah Color and Multiphase Image Segmentation

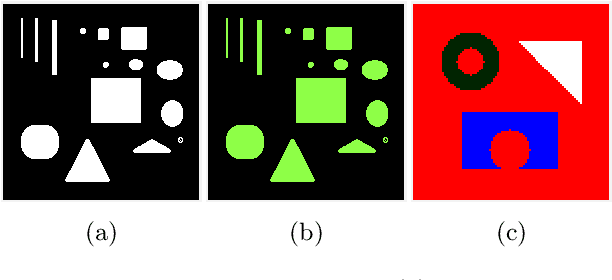
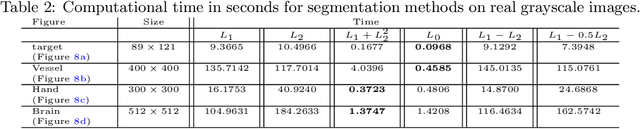
In a class of piecewise-constant image segmentation models, we incorporate a weighted difference of anisotropic and isotropic total variation (TV) to regularize the partition boundaries in an image. To deal with the weighted anisotropic-isotropic TV, we apply the difference-of-convex algorithm (DCA), where the subproblems can be minimized by the primal-dual hybrid gradient method (PDHG). As a result, we are able to design an alternating minimization algorithm to solve the proposed image segmentation models. The models and algorithms are further extended to segment color images and to perform multiphase segmentation. In the numerical experiments, we compare our proposed models with the Chan-Vese models that use either anisotropic or isotropic TV and the two-stage segmentation methods (denoising and then thresholding) on various images. The results demonstrate the effectiveness and robustness of incorporating weighted anisotropic-isotropic TV in image segmentation.