On the exact recovery of sparse signals via conic relaxations
Paper and Code
Mar 15, 2016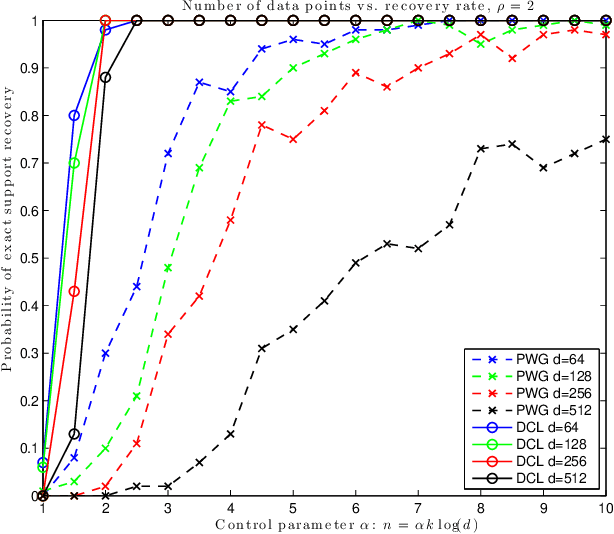
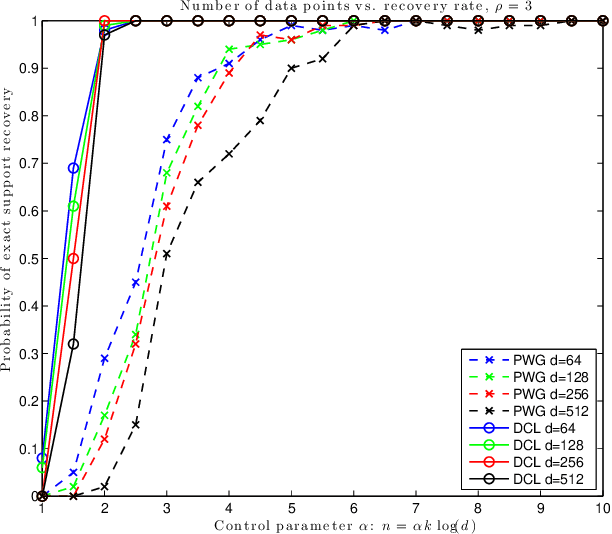
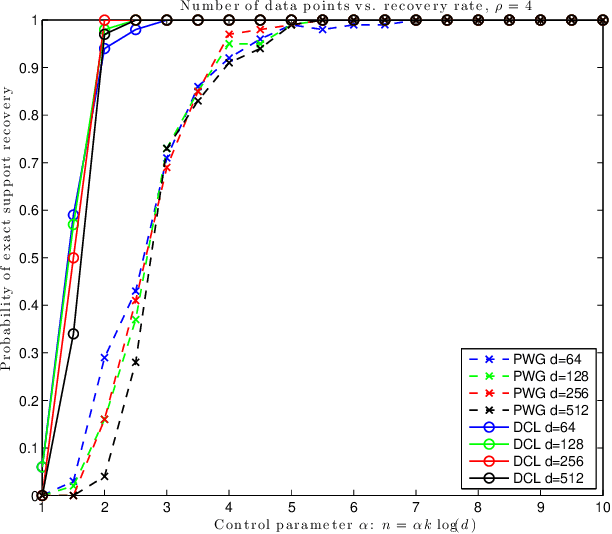
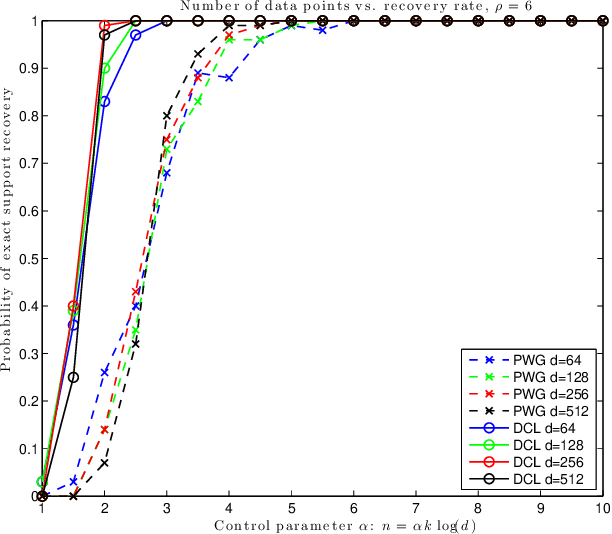
In this note we compare two recently proposed semidefinite relaxations for the sparse linear regression problem by Pilanci, Wainwright and El Ghaoui (Sparse learning via boolean relaxations, 2015) and Dong, Chen and Linderoth (Relaxation vs. Regularization A conic optimization perspective of statistical variable selection, 2015). We focus on the cardinality constrained formulation, and prove that the relaxation proposed by Dong, etc. is theoretically no weaker than the one proposed by Pilanci, etc. Therefore any sufficient condition of exact recovery derived by Pilanci can be readily applied to the other relaxation, including their results on high probability recovery for Gaussian ensemble. Finally we provide empirical evidence that the relaxation by Dong, etc. requires much fewer observations to guarantee the recovery of true support.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge