Regularization vs. Relaxation: A conic optimization perspective of statistical variable selection
Paper and Code
Oct 20, 2015
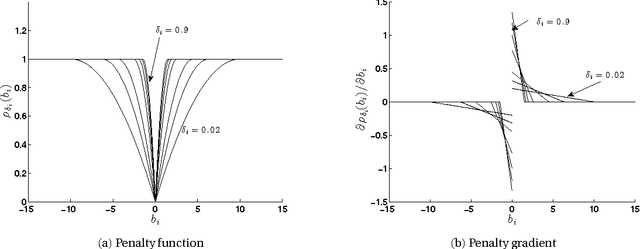
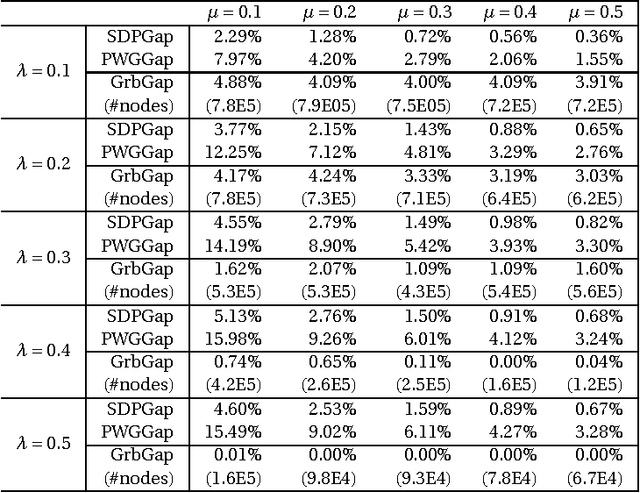
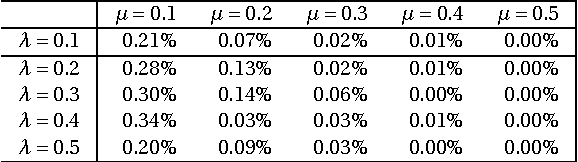
Variable selection is a fundamental task in statistical data analysis. Sparsity-inducing regularization methods are a popular class of methods that simultaneously perform variable selection and model estimation. The central problem is a quadratic optimization problem with an l0-norm penalty. Exactly enforcing the l0-norm penalty is computationally intractable for larger scale problems, so dif- ferent sparsity-inducing penalty functions that approximate the l0-norm have been introduced. In this paper, we show that viewing the problem from a convex relaxation perspective offers new insights. In particular, we show that a popular sparsity-inducing concave penalty function known as the Minimax Concave Penalty (MCP), and the reverse Huber penalty derived in a recent work by Pilanci, Wainwright and Ghaoui, can both be derived as special cases of a lifted convex relaxation called the perspective relaxation. The optimal perspective relaxation is a related minimax problem that balances the overall convexity and tightness of approximation to the l0 norm. We show it can be solved by a semidefinite relaxation. Moreover, a probabilistic interpretation of the semidefinite relaxation reveals connections with the boolean quadric polytope in combinatorial optimization. Finally by reformulating the l0-norm pe- nalized problem as a two-level problem, with the inner level being a Max-Cut problem, our proposed semidefinite relaxation can be realized by replacing the inner level problem with its semidefinite relaxation studied by Goemans and Williamson. This interpretation suggests using the Goemans-Williamson rounding procedure to find approximate solutions to the l0-norm penalized problem. Numerical experiments demonstrate the tightness of our proposed semidefinite relaxation, and the effectiveness of finding approximate solutions by Goemans-Williamson rounding.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge