Sample Efficient Linear Meta-Learning by Alternating Minimization
Paper and Code
May 18, 2021
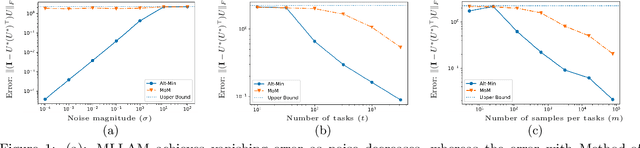
Meta-learning synthesizes and leverages the knowledge from a given set of tasks to rapidly learn new tasks using very little data. Meta-learning of linear regression tasks, where the regressors lie in a low-dimensional subspace, is an extensively-studied fundamental problem in this domain. However, existing results either guarantee highly suboptimal estimation errors, or require $\Omega(d)$ samples per task (where $d$ is the data dimensionality) thus providing little gain over separately learning each task. In this work, we study a simple alternating minimization method (MLLAM), which alternately learns the low-dimensional subspace and the regressors. We show that, for a constant subspace dimension MLLAM obtains nearly-optimal estimation error, despite requiring only $\Omega(\log d)$ samples per task. However, the number of samples required per task grows logarithmically with the number of tasks. To remedy this in the low-noise regime, we propose a novel task subset selection scheme that ensures the same strong statistical guarantee as MLLAM, even with bounded number of samples per task for arbitrarily large number of tasks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge