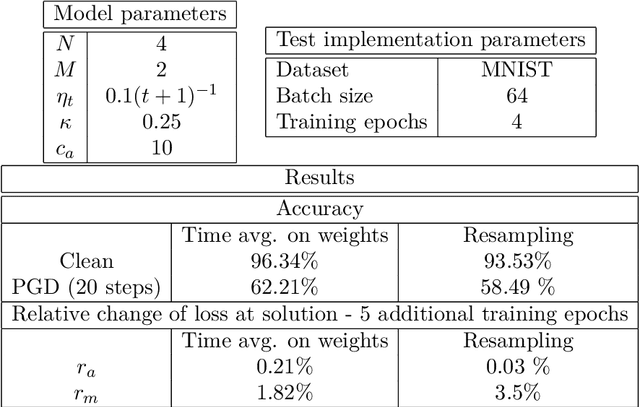
On adversarial robustness and the use of Wasserstein ascent-descent dynamics to enforce it

We propose iterative algorithms to solve adversarial problems in a variety of supervised learning settings of interest. Our algorithms, which can be interpreted as suitable ascent-descent dynamics in Wasserstein spaces, take the form of a system of interacting particles. These interacting particle dynamics are shown to converge toward appropriate mean-field limit equations in certain large number of particles regimes. In turn, we prove that, under certain regularity assumptions, these mean-field equations converge, in the large time limit, toward approximate Nash equilibria of the original adversarial learning problems. We present results for nonconvex-nonconcave settings, as well as for nonconvex-concave ones. Numerical experiments illustrate our results.

On the regularized risk of distributionally robust learning over deep neural networks

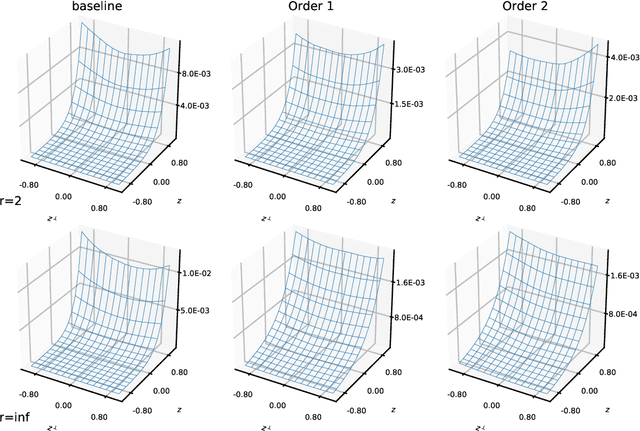
In this paper we explore the relation between distributionally robust learning and different forms of regularization to enforce robustness of deep neural networks. In particular, starting from a concrete min-max distributionally robust problem, and using tools from optimal transport theory, we derive first order and second order approximations to the distributionally robust problem in terms of appropriate regularized risk minimization problems. In the context of deep ResNet models, we identify the structure of the resulting regularization problems as mean-field optimal control problems where the number and dimension of state variables is within a dimension-free factor of the dimension of the original unrobust problem. Using the Pontryagin maximum principles associated to these problems we motivate a family of scalable algorithms for the training of robust neural networks. Our analysis recovers some results and algorithms known in the literature (in settings explained throughout the paper) and provides many other theoretical and algorithmic insights that to our knowledge are novel. In our analysis we employ tools that we deem useful for a future analysis of more general adversarial learning problems.