Tensor-on-Tensor Regression: Riemannian Optimization, Over-parameterization, Statistical-computational Gap, and Their Interplay
Paper and Code
Jun 17, 2022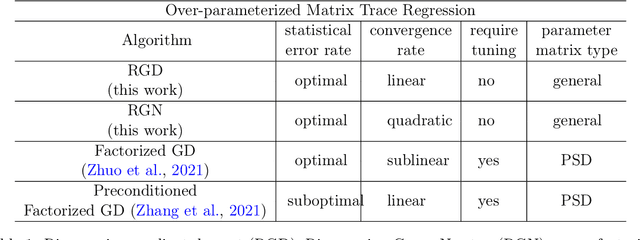
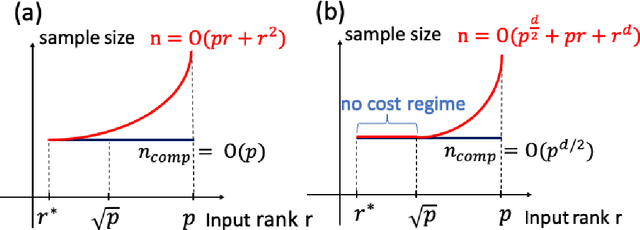
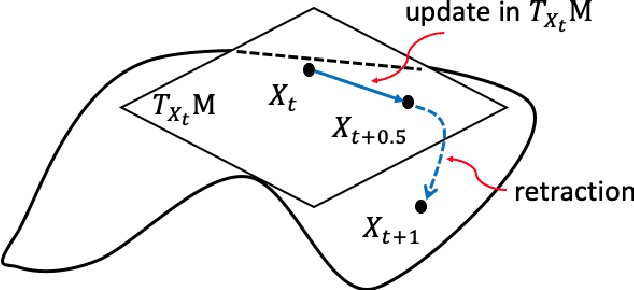
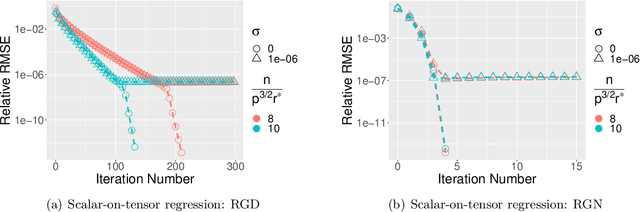
We study the tensor-on-tensor regression, where the goal is to connect tensor responses to tensor covariates with a low Tucker rank parameter tensor/matrix without the prior knowledge of its intrinsic rank. We propose the Riemannian gradient descent (RGD) and Riemannian Gauss-Newton (RGN) methods and cope with the challenge of unknown rank by studying the effect of rank over-parameterization. We provide the first convergence guarantee for the general tensor-on-tensor regression by showing that RGD and RGN respectively converge linearly and quadratically to a statistically optimal estimate in both rank correctly-parameterized and over-parameterized settings. Our theory reveals an intriguing phenomenon: Riemannian optimization methods naturally adapt to over-parameterization without modifications to their implementation. We also give the first rigorous evidence for the statistical-computational gap in scalar-on-tensor regression under the low-degree polynomials framework. Our theory demonstrates a ``blessing of statistical-computational gap" phenomenon: in a wide range of scenarios in tensor-on-tensor regression for tensors of order three or higher, the computationally required sample size matches what is needed by moderate rank over-parameterization when considering computationally feasible estimators, while there are no such benefits in the matrix settings. This shows moderate rank over-parameterization is essentially ``cost-free" in terms of sample size in tensor-on-tensor regression of order three or higher. Finally, we conduct simulation studies to show the advantages of our proposed methods and to corroborate our theoretical findings.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge