Benjamin Mark
Context-dependent self-exciting point processes: models, methods, and risk bounds in high dimensions
Mar 16, 2020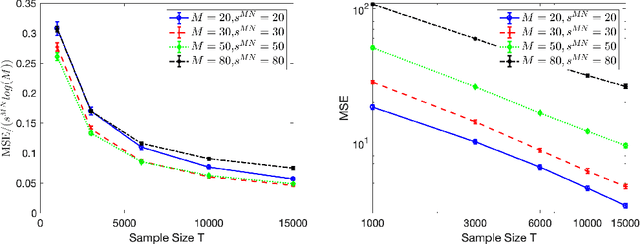
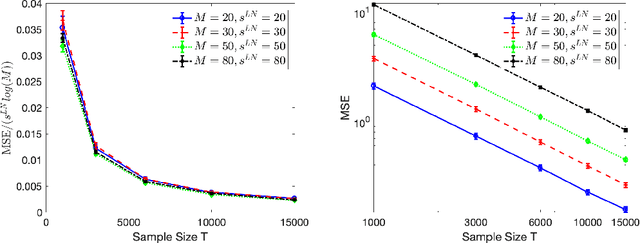
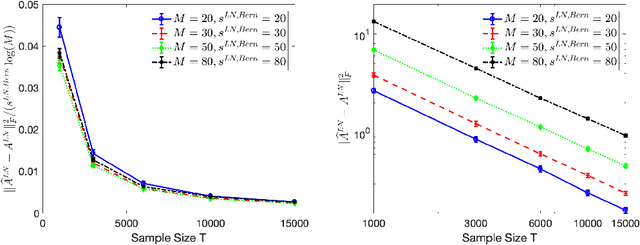
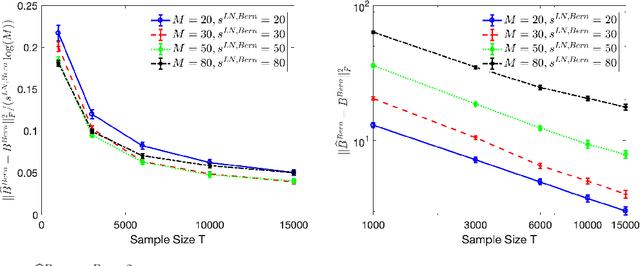
Abstract:High-dimensional autoregressive point processes model how current events trigger or inhibit future events, such as activity by one member of a social network can affect the future activity of his or her neighbors. While past work has focused on estimating the underlying network structure based solely on the times at which events occur on each node of the network, this paper examines the more nuanced problem of estimating context-dependent networks that reflect how features associated with an event (such as the content of a social media post) modulate the strength of influences among nodes. Specifically, we leverage ideas from compositional time series and regularization methods in machine learning to conduct network estimation for high-dimensional marked point processes. Two models and corresponding estimators are considered in detail: an autoregressive multinomial model suited to categorical marks and a logistic-normal model suited to marks with mixed membership in different categories. Importantly, the logistic-normal model leads to a convex negative log-likelihood objective and captures dependence across categories. We provide theoretical guarantees for both estimators, which we validate by simulations and a synthetic data-generating model. We further validate our methods through two real data examples and demonstrate the advantages and disadvantages of both approaches.
Estimating Network Structure from Incomplete Event Data
Nov 07, 2018
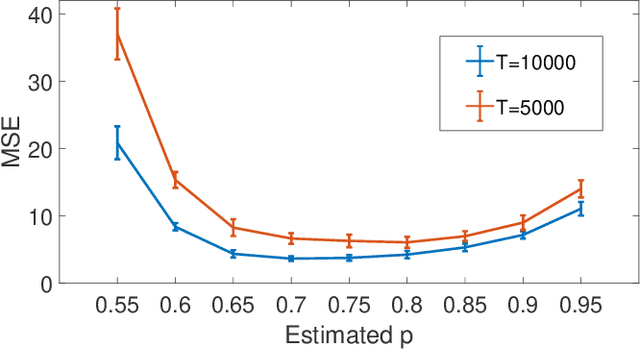

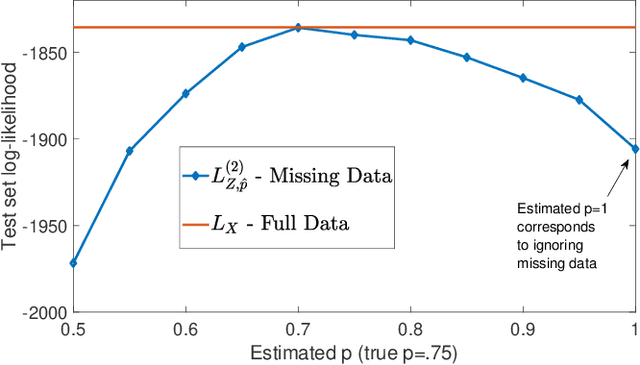
Abstract:Multivariate Bernoulli autoregressive (BAR) processes model time series of events in which the likelihood of current events is determined by the times and locations of past events. These processes can be used to model nonlinear dynamical systems corresponding to criminal activity, responses of patients to different medical treatment plans, opinion dynamics across social networks, epidemic spread, and more. Past work examines this problem under the assumption that the event data is complete, but in many cases only a fraction of events are observed. Incomplete observations pose a significant challenge in this setting because the unobserved events still govern the underlying dynamical system. In this work, we develop a novel approach to estimating the parameters of a BAR process in the presence of unobserved events via an unbiased estimator of the complete data log-likelihood function. We propose a computationally efficient estimation algorithm which approximates this estimator via Taylor series truncation and establish theoretical results for both the statistical error and optimization error of our algorithm. We further justify our approach by testing our method on both simulated data and a real data set consisting of crimes recorded by the city of Chicago.
Graph-based regularization for regression problems with highly-correlated designs
Jun 05, 2018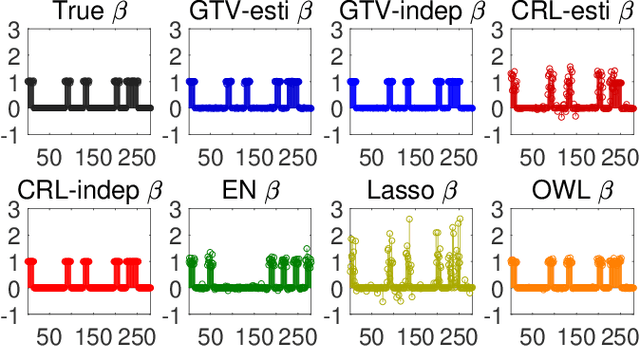

Abstract:Sparse models for high-dimensional linear regression and machine learning have received substantial attention over the past two decades. Model selection, or determining which features or covariates are the best explanatory variables, is critical to the interpretability of a learned model. Much of the current literature assumes that covariates are only mildly correlated. However, in modern applications ranging from functional MRI to genome-wide association studies, covariates are highly correlated and do not exhibit key properties (such as the restricted eigenvalue condition, RIP, or other related assumptions). This paper considers a high-dimensional regression setting in which a graph governs both correlations among the covariates and the similarity among regression coefficients. Using side information about the strength of correlations among features, we form a graph with edge weights corresponding to pairwise covariances. This graph is used to define a graph total variation regularizer that promotes similar weights for highly correlated features. The graph structure encapsulated by this regularizer helps precondition correlated features to yield provably accurate estimates. Using graph-based regularizers to develop theoretical guarantees for highly-correlated covariates has not been previously examined. This paper shows how our proposed graph-based regularization yields mean-squared error guarantees for a broad range of covariance graph structures and correlation strengths which in many cases are optimal by imposing additional structure on $\beta^{\star}$ which encourages \emph{alignment} with the covariance graph. Our proposed approach outperforms other state-of-the-art methods for highly-correlated design in a variety of experiments on simulated and real fMRI data.
Network Estimation from Point Process Data
Feb 13, 2018



Abstract:Consider observing a collection of discrete events within a network that reflect how network nodes influence one another. Such data are common in spike trains recorded from biological neural networks, interactions within a social network, and a variety of other settings. Data of this form may be modeled as self-exciting point processes, in which the likelihood of future events depends on the past events. This paper addresses the problem of estimating self-excitation parameters and inferring the underlying functional network structure from self-exciting point process data. Past work in this area was limited by strong assumptions which are addressed by the novel approach here. Specifically, in this paper we (1) incorporate saturation in a point process model which both ensures stability and models non-linear thresholding effects; (2) impose general low-dimensional structural assumptions that include sparsity, group sparsity and low-rankness that allows bounds to be developed in the high-dimensional setting; and (3) incorporate long-range memory effects through moving average and higher-order auto-regressive components. Using our general framework, we provide a number of novel theoretical guarantees for high-dimensional self-exciting point processes that reflect the role played by the underlying network structure and long-term memory. We also provide simulations and real data examples to support our methodology and main results.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge