Estimating Network Structure from Incomplete Event Data
Paper and Code
Nov 07, 2018
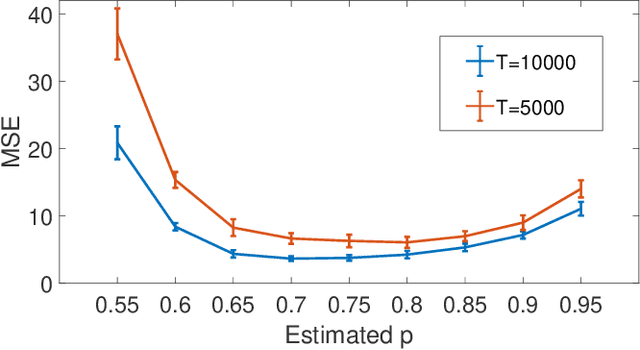

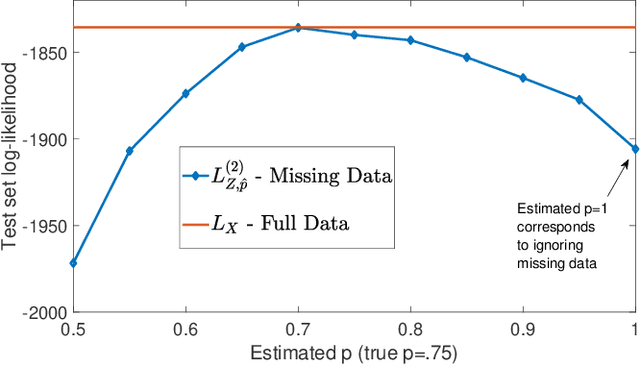
Multivariate Bernoulli autoregressive (BAR) processes model time series of events in which the likelihood of current events is determined by the times and locations of past events. These processes can be used to model nonlinear dynamical systems corresponding to criminal activity, responses of patients to different medical treatment plans, opinion dynamics across social networks, epidemic spread, and more. Past work examines this problem under the assumption that the event data is complete, but in many cases only a fraction of events are observed. Incomplete observations pose a significant challenge in this setting because the unobserved events still govern the underlying dynamical system. In this work, we develop a novel approach to estimating the parameters of a BAR process in the presence of unobserved events via an unbiased estimator of the complete data log-likelihood function. We propose a computationally efficient estimation algorithm which approximates this estimator via Taylor series truncation and establish theoretical results for both the statistical error and optimization error of our algorithm. We further justify our approach by testing our method on both simulated data and a real data set consisting of crimes recorded by the city of Chicago.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge