Prediction in the presence of response-dependent missing labels
Paper and Code
Mar 25, 2021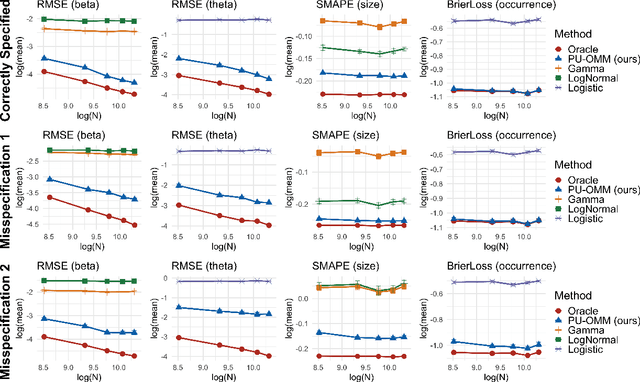
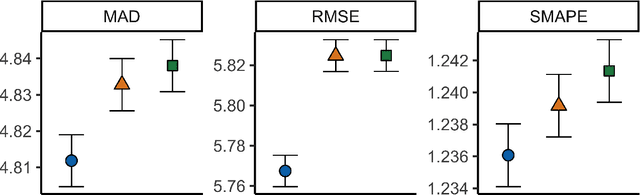
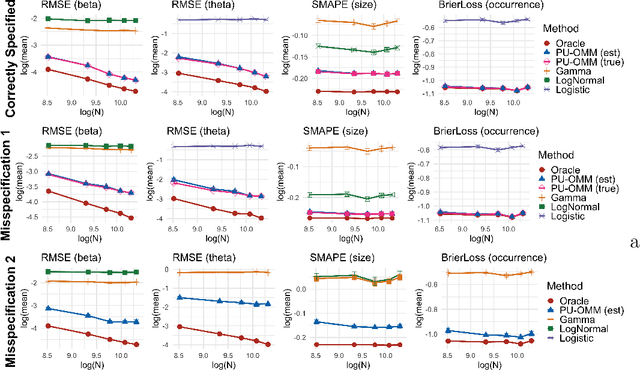
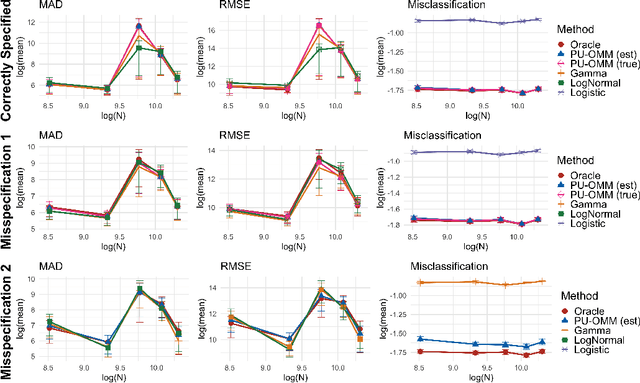
In a variety of settings, limitations of sensing technologies or other sampling mechanisms result in missing labels, where the likelihood of a missing label in the training set is an unknown function of the data. For example, satellites used to detect forest fires cannot sense fires below a certain size threshold. In such cases, training datasets consist of positive and pseudo-negative observations where pseudo-negative observations can be either true negatives or undetected positives with small magnitudes. We develop a new methodology and non-convex algorithm P(ositive) U(nlabeled) - O(ccurrence) M(agnitude) M(ixture) which jointly estimates the occurrence and detection likelihood of positive samples, utilizing prior knowledge of the detection mechanism. Our approach uses ideas from positive-unlabeled (PU)-learning and zero-inflated models that jointly estimate the magnitude and occurrence of events. We provide conditions under which our model is identifiable and prove that even though our approach leads to a non-convex objective, any local minimizer has optimal statistical error (up to a log term) and projected gradient descent has geometric convergence rates. We demonstrate on both synthetic data and a California wildfire dataset that our method out-performs existing state-of-the-art approaches.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge