Adaptive Batching for Gaussian Process Surrogates with Application in Noisy Level Set Estimation

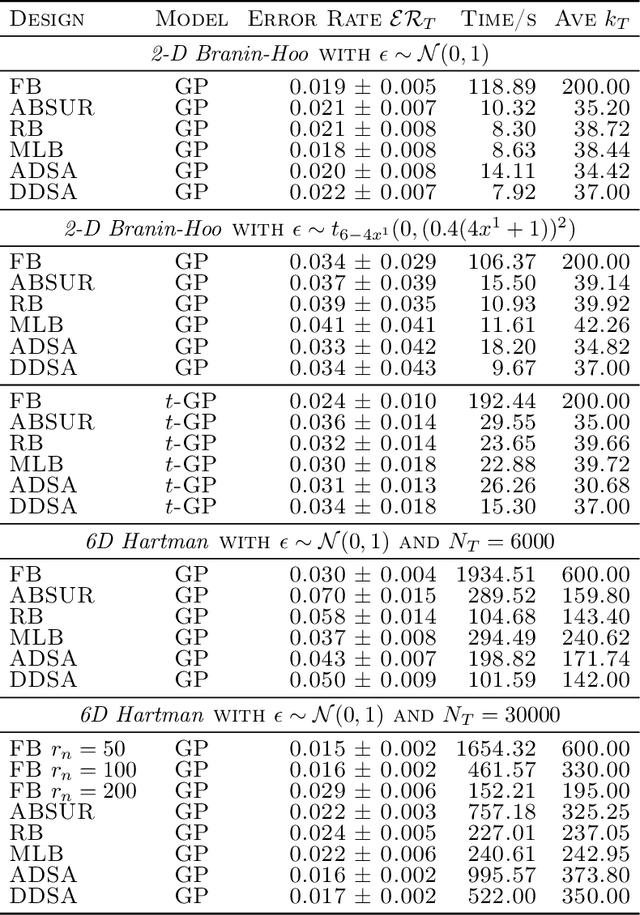
We develop adaptive replicated designs for Gaussian process metamodels of stochastic experiments. Adaptive batching is a natural extension of sequential design heuristics with the benefit of replication growing as response features are learned, inputs concentrate, and the metamodeling overhead rises. Motivated by the problem of learning the level set of the mean simulator response we develop four novel schemes: Multi-Level Batching (MLB), Ratchet Batching (RB), Adaptive Batched Stepwise Uncertainty Reduction (ABSUR), Adaptive Design with Stepwise Allocation (ADSA) and Deterministic Design with Stepwise Allocation (DDSA). Our algorithms simultaneously (MLB, RB and ABSUR) or sequentially (ADSA and DDSA) determine the sequential design inputs and the respective number of replicates. Illustrations using synthetic examples and an application in quantitative finance (Bermudan option pricing via Regression Monte Carlo) show that adaptive batching brings significant computational speed-ups with minimal loss of modeling fidelity.

Evaluating Gaussian Process Metamodels and Sequential Designs for Noisy Level Set Estimation

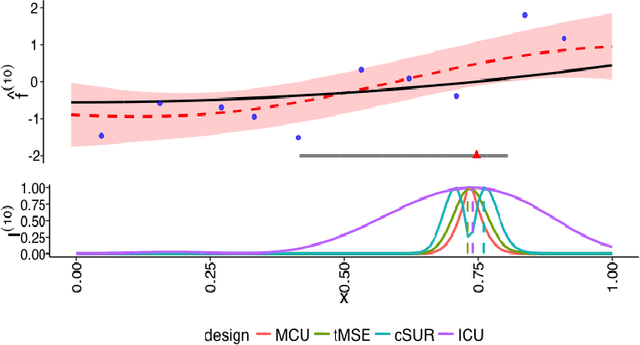
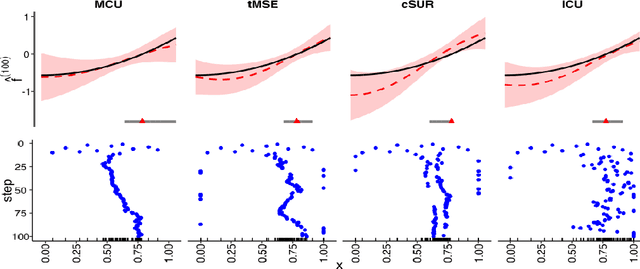
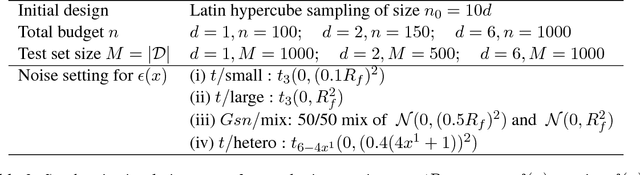
We consider the problem of learning the level set for which a noisy black-box function exceeds a given threshold. To efficiently reconstruct the level set, we investigate Gaussian process (GP) metamodels. Our focus is on strongly stochastic samplers, in particular with heavy-tailed simulation noise and low signal-to-noise ratio. To guard against noise misspecification, we assess the performance of three variants: (i) GPs with Student-$t$ observations; (ii) Student-$t$ processes (TPs); and (iii) classification GPs modeling the sign of the response. As a fourth extension, we study GP surrogates with monotonicity constraints that are relevant when the level set is known to be connected. In conjunction with these metamodels, we analyze several acquisition functions for guiding the sequential experimental designs, extending existing stepwise uncertainty reduction criteria to the stochastic contour-finding context. This also motivates our development of (approximate) updating formulas to efficiently compute such acquisition functions. Our schemes are benchmarked by using a variety of synthetic experiments in 1--6 dimensions. We also consider an application of level set estimation for determining the optimal exercise policy and valuation of Bermudan options in finance.