Extreme Scenario Selection in Day-Ahead Power Grid Operational Planning

We propose and analyze the application of statistical functional depth metrics for the selection of extreme scenarios in day-ahead grid planning. Our primary motivation is screening of probabilistic scenarios for realized load and renewable generation, in order to identify scenarios most relevant for operational risk mitigation. To handle the high-dimensionality of the scenarios across asset classes and intra-day periods, we employ functional measures of depth to sub-select outlying scenarios that are most likely to be the riskiest for the grid operation. We investigate a range of functional depth measures, as well as a range of operational risks, including load shedding, operational costs, reserves shortfall and variable renewable energy curtailment. The effectiveness of the proposed screening approach is demonstrated through a case study on the realistic Texas-7k grid.

Evaluating Gaussian Process Metamodels and Sequential Designs for Noisy Level Set Estimation

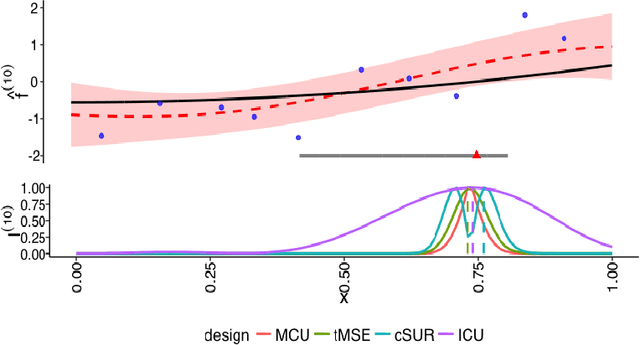
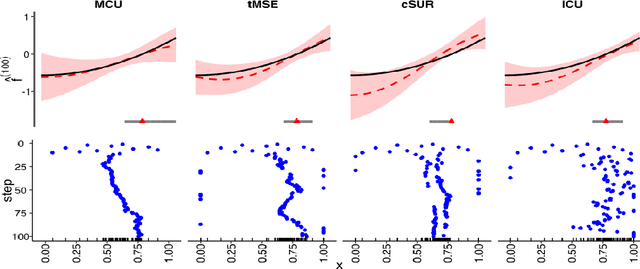
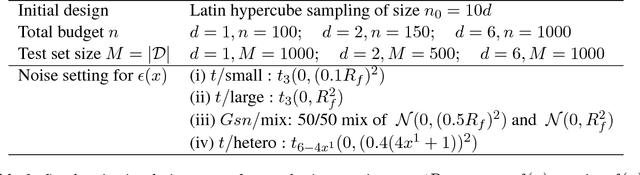
We consider the problem of learning the level set for which a noisy black-box function exceeds a given threshold. To efficiently reconstruct the level set, we investigate Gaussian process (GP) metamodels. Our focus is on strongly stochastic samplers, in particular with heavy-tailed simulation noise and low signal-to-noise ratio. To guard against noise misspecification, we assess the performance of three variants: (i) GPs with Student-$t$ observations; (ii) Student-$t$ processes (TPs); and (iii) classification GPs modeling the sign of the response. As a fourth extension, we study GP surrogates with monotonicity constraints that are relevant when the level set is known to be connected. In conjunction with these metamodels, we analyze several acquisition functions for guiding the sequential experimental designs, extending existing stepwise uncertainty reduction criteria to the stochastic contour-finding context. This also motivates our development of (approximate) updating formulas to efficiently compute such acquisition functions. Our schemes are benchmarked by using a variety of synthetic experiments in 1--6 dimensions. We also consider an application of level set estimation for determining the optimal exercise policy and valuation of Bermudan options in finance.

Generalized Probabilistic Bisection for Stochastic Root-Finding

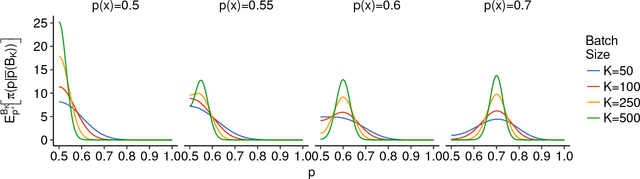
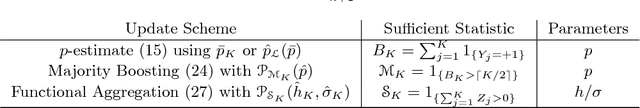
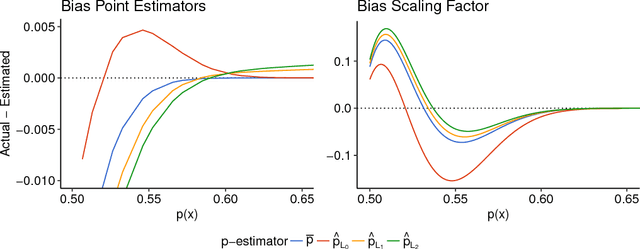
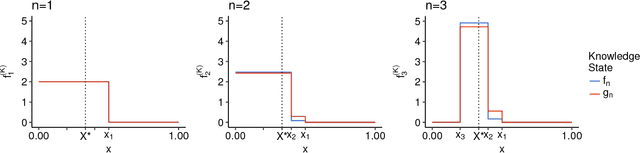
We consider numerical schemes for root finding of noisy responses through generalizing the Probabilistic Bisection Algorithm (PBA) to the more practical context where the sampling distribution is unknown and location-dependent. As in standard PBA, we rely on a knowledge state for the approximate posterior of the root location. To implement the corresponding Bayesian updating, we also carry out inference of oracle accuracy, namely learning the probability of correct response. To this end we utilize batched querying in combination with a variety of frequentist and Bayesian estimators based on majority vote, as well as the underlying functional responses, if available. For guiding sampling selection we investigate both Information Directed sampling, as well as Quantile sampling. Our numerical experiments show that these strategies perform quite differently; in particular we demonstrate the efficiency of randomized quantile sampling which is reminiscent of Thompson sampling. Our work is motivated by the root-finding sub-routine in pricing of Bermudan financial derivatives, illustrated in the last section of the paper.