Probabilistic Bisection with Spatial Metamodels

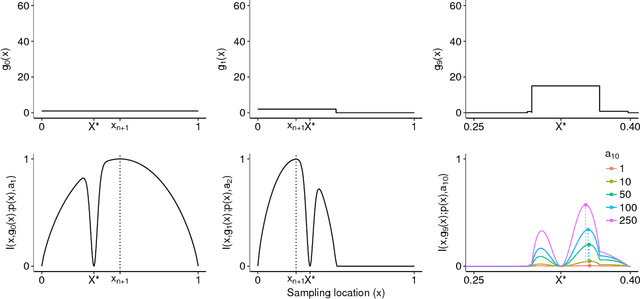
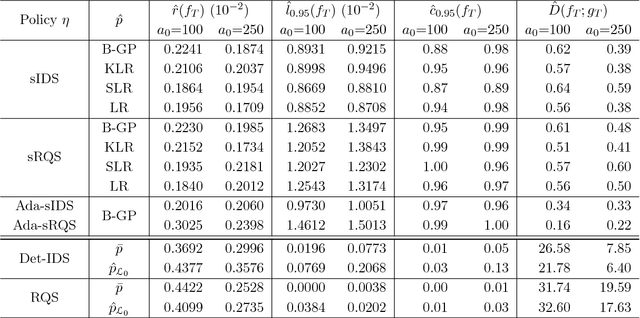
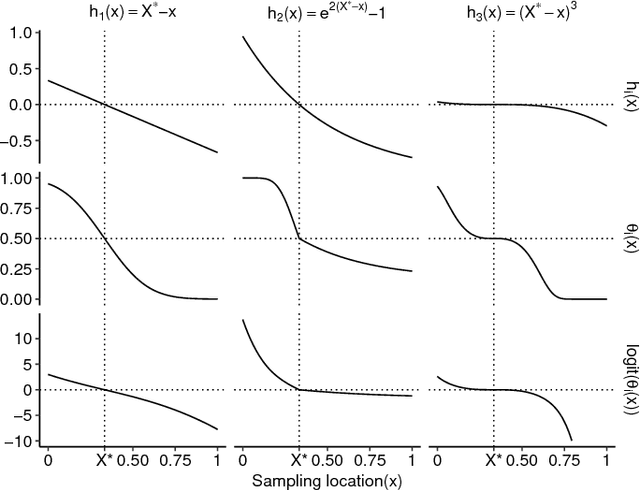
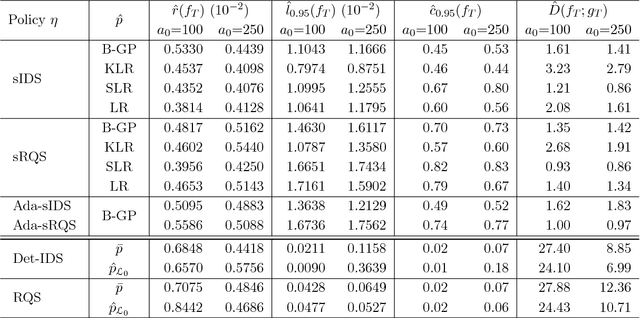
Probabilistic Bisection Algorithm performs root finding based on knowledge acquired from noisy oracle responses. We consider the generalized PBA setting (G-PBA) where the statistical distribution of the oracle is unknown and location-dependent, so that model inference and Bayesian knowledge updating must be performed simultaneously. To this end, we propose to leverage the spatial structure of a typical oracle by constructing a statistical surrogate for the underlying logistic regression step. We investigate several non-parametric surrogates, including Binomial Gaussian Processes (B-GP), Polynomial, Kernel, and Spline Logistic Regression. In parallel, we develop sampling policies that adaptively balance learning the oracle distribution and learning the root. One of our proposals mimics active learning with B-GPs and provides a novel look-ahead predictive variance formula. The resulting gains of our Spatial PBA algorithm relative to earlier G-PBA models are illustrated with synthetic examples and a challenging stochastic root finding problem from Bermudan option pricing.

Generalized Probabilistic Bisection for Stochastic Root-Finding

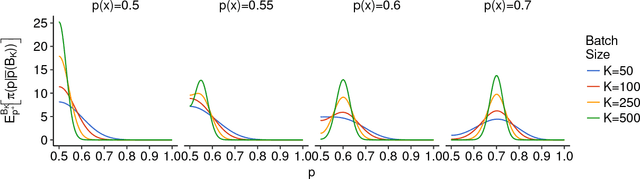
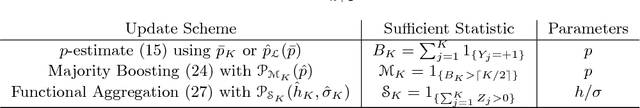
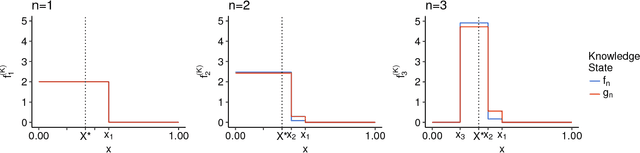
We consider numerical schemes for root finding of noisy responses through generalizing the Probabilistic Bisection Algorithm (PBA) to the more practical context where the sampling distribution is unknown and location-dependent. As in standard PBA, we rely on a knowledge state for the approximate posterior of the root location. To implement the corresponding Bayesian updating, we also carry out inference of oracle accuracy, namely learning the probability of correct response. To this end we utilize batched querying in combination with a variety of frequentist and Bayesian estimators based on majority vote, as well as the underlying functional responses, if available. For guiding sampling selection we investigate both Information Directed sampling, as well as Quantile sampling. Our numerical experiments show that these strategies perform quite differently; in particular we demonstrate the efficiency of randomized quantile sampling which is reminiscent of Thompson sampling. Our work is motivated by the root-finding sub-routine in pricing of Bermudan financial derivatives, illustrated in the last section of the paper.