Rademacher Complexity and Generalization Performance of Multi-category Margin Classifiers
Paper and Code
Dec 03, 2018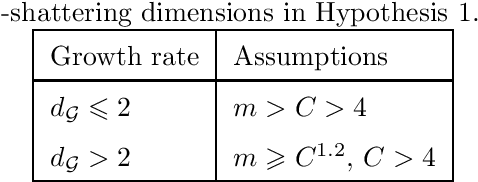
One of the main open problems in the theory of multi-category margin classification is the form of the optimal dependency of a guaranteed risk on the number C of categories, the sample size m and the margin parameter gamma. From a practical point of view, the theoretical analysis of generalization performance contributes to the development of new learning algorithms. In this paper, we focus only on the theoretical aspect of the question posed. More precisely, under minimal learnability assumptions, we derive a new risk bound for multi-category margin classifiers. We improve the dependency on C over the state of the art when the margin loss function considered satisfies the Lipschitz condition. We start with the basic supremum inequality that involves a Rademacher complexity as a capacity measure. This capacity measure is then linked to the metric entropy through the chaining method. In this context, our improvement is based on the introduction of a new combinatorial metric entropy bound.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge