Linear chain conditional random fields, hidden Markov models, and related classifiers

Practitioners use Hidden Markov Models (HMMs) in different problems for about sixty years. Besides, Conditional Random Fields (CRFs) are an alternative to HMMs and appear in the literature as different and somewhat concurrent models. We propose two contributions. First, we show that basic Linear-Chain CRFs (LC-CRFs), considered as different from the HMMs, are in fact equivalent to them in the sense that for each LC-CRF there exists a HMM - that we specify - whom posterior distribution is identical to the given LC-CRF. Second, we show that it is possible to reformulate the generative Bayesian classifiers Maximum Posterior Mode (MPM) and Maximum a Posteriori (MAP) used in HMMs, as discriminative ones. The last point is of importance in many fields, especially in Natural Language Processing (NLP), as it shows that in some situations dropping HMMs in favor of CRFs was not necessary.

Deriving discriminative classifiers from generative models

We deal with Bayesian generative and discriminative classifiers. Given a model distribution $p(x, y)$, with the observation $y$ and the target $x$, one computes generative classifiers by firstly considering $p(x, y)$ and then using the Bayes rule to calculate $p(x | y)$. A discriminative model is directly given by $p(x | y)$, which is used to compute discriminative classifiers. However, recent works showed that the Bayesian Maximum Posterior classifier defined from the Naive Bayes (NB) or Hidden Markov Chain (HMC), both generative models, can also match the discriminative classifier definition. Thus, there are situations in which dividing classifiers into "generative" and "discriminative" is somewhat misleading. Indeed, such a distinction is rather related to the way of computing classifiers, not to the classifiers themselves. We present a general theoretical result specifying how a generative classifier induced from a generative model can also be computed in a discriminative way from the same model. Examples of NB and HMC are found again as particular cases, and we apply the general result to two original extensions of NB, and two extensions of HMC, one of which being original. Finally, we shortly illustrate the interest of the new discriminative way of computing classifiers in the Natural Language Processing (NLP) framework.

On equivalence between linear-chain conditional random fields and hidden Markov chains

Practitioners successfully use hidden Markov chains (HMCs) in different problems for about sixty years. HMCs belong to the family of generative models and they are often compared to discriminative models, like conditional random fields (CRFs). Authors usually consider CRFs as quite different from HMCs, and CRFs are often presented as interesting alternative to HMCs. In some areas, like natural language processing (NLP), discriminative models have completely supplanted generative models. However, some recent results show that both families of models are not so different, and both of them can lead to identical processing power. In this paper we compare the simple linear-chain CRFs to the basic HMCs. We show that HMCs are identical to CRFs in that for each CRF we explicitly construct an HMC having the same posterior distribution. Therefore, HMCs and linear-chain CRFs are not different but just differently parametrized models.

Improving usual Naive Bayes classifier performances with Neural Naive Bayes based models

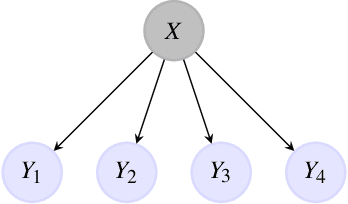
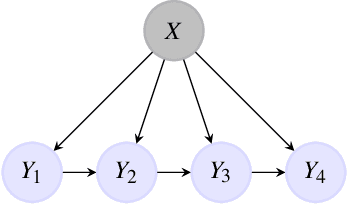
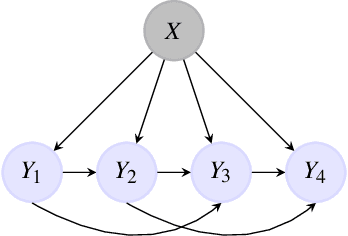
Naive Bayes is a popular probabilistic model appreciated for its simplicity and interpretability. However, the usual form of the related classifier suffers from two major problems. First, as caring about the observations' law, it cannot consider complex features. Moreover, it considers the conditional independence of the observations given the hidden variable. This paper introduces the original Neural Naive Bayes, modeling the parameters of the classifier induced from the Naive Bayes with neural network functions. This allows to correct the first problem. We also introduce new Neural Pooled Markov Chain models, alleviating the independence condition. We empirically study the benefits of these models for Sentiment Analysis, dividing the error rate of the usual classifier by 4.5 on the IMDB dataset with the FastText embedding.

Introducing the Hidden Neural Markov Chain framework

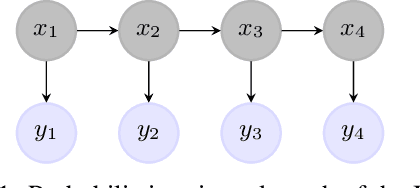
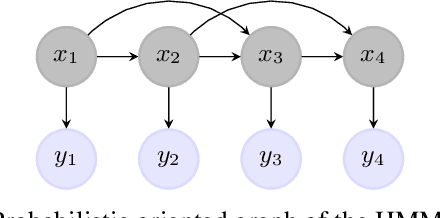
Nowadays, neural network models achieve state-of-the-art results in many areas as computer vision or speech processing. For sequential data, especially for Natural Language Processing (NLP) tasks, Recurrent Neural Networks (RNNs) and their extensions, the Long Short Term Memory (LSTM) network and the Gated Recurrent Unit (GRU), are among the most used models, having a "term-to-term" sequence processing. However, if many works create extensions and improvements of the RNN, few have focused on developing other ways for sequential data processing with neural networks in a "term-to-term" way. This paper proposes the original Hidden Neural Markov Chain (HNMC) framework, a new family of sequential neural models. They are not based on the RNN but on the Hidden Markov Model (HMM), a probabilistic graphical model. This neural extension is possible thanks to the recent Entropic Forward-Backward algorithm for HMM restoration. We propose three different models: the classic HNMC, the HNMC2, and the HNMC-CN. After describing our models' whole construction, we compare them with classic RNN and Bidirectional RNN (BiRNN) models for some sequence labeling tasks: Chunking, Part-Of-Speech Tagging, and Named Entity Recognition. For every experiment, whatever the architecture or the embedding method used, one of our proposed models has the best results. It shows this new neural sequential framework's potential, which can open the way to new models, and might eventually compete with the prevalent BiLSTM and BiGRU.

Highly Fast Text Segmentation With Pairwise Markov Chains

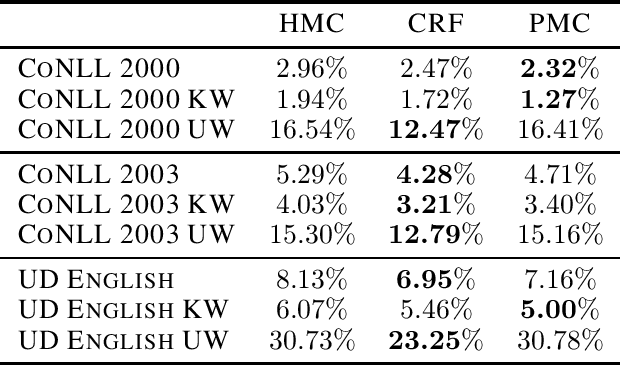
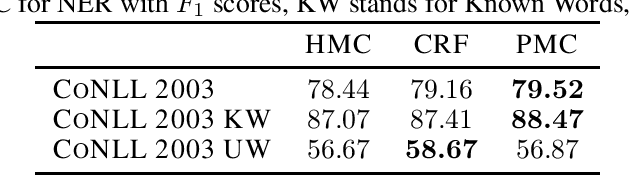
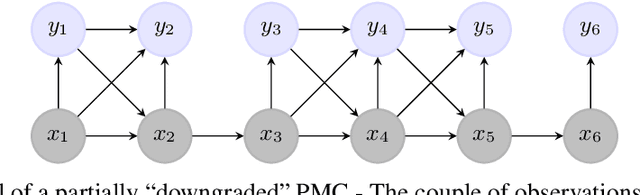
Natural Language Processing (NLP) models' current trend consists of using increasingly more extra-data to build the best models as possible. It implies more expensive computational costs and training time, difficulties for deployment, and worries about these models' carbon footprint reveal a critical problem in the future. Against this trend, our goal is to develop NLP models requiring no extra-data and minimizing training time. To do so, in this paper, we explore Markov chain models, Hidden Markov Chain (HMC) and Pairwise Markov Chain (PMC), for NLP segmentation tasks. We apply these models for three classic applications: POS Tagging, Named-Entity-Recognition, and Chunking. We develop an original method to adapt these models for text segmentation's specific challenges to obtain relevant performances with very short training and execution times. PMC achieves equivalent results to those obtained by Conditional Random Fields (CRF), one of the most applied models for these tasks when no extra-data are used. Moreover, PMC has training times 30 times shorter than the CRF ones, which validates this model given our objectives.

Using the Naive Bayes as a discriminative classifier

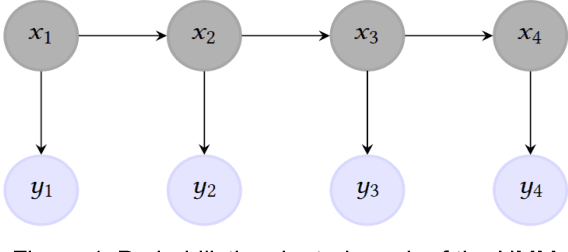
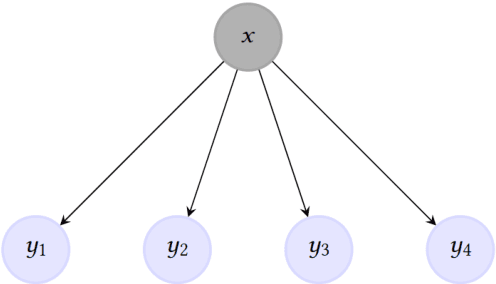
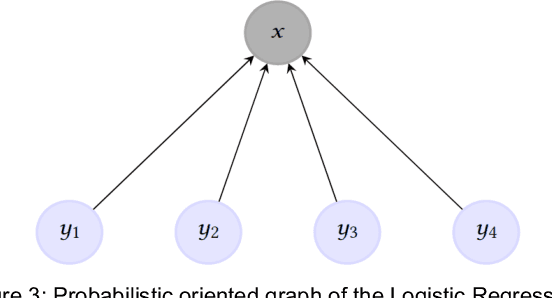
For classification tasks, probabilistic models can be categorized into two disjoint classes: generative or discriminative. It depends on the posterior probability computation of the label $x$ given the observation $y$, $p(x | y)$. On the one hand, generative classifiers, like the Naive Bayes or the Hidden Markov Model (HMM), need the computation of the joint probability $p(x, y)$, before using the Bayes rule to compute $p(x | y)$. On the other hand, discriminative classifiers compute $p(x | y)$ directly, regardless of the observations' law. They are intensively used nowadays, with models as Logistic Regression, Conditional Random Fields (CRF), and Artificial Neural Networks. However, the recent Entropic Forward-Backward algorithm shows that the HMM, considered as a generative model, can also match the discriminative one's definition. This example leads to question if it is the case for other generative models. In this paper, we show that the Naive Bayes classifier can also match the discriminative classifier definition, so it can be used in either a generative or a discriminative way. Moreover, this observation also discusses the notion of Generative-Discriminative pairs, linking, for example, Naive Bayes and Logistic Regression, or HMM and CRF. Related to this point, we show that the Logistic Regression can be viewed as a particular case of the Naive Bayes used in a discriminative way.

Hidden Markov Chains, Entropic Forward-Backward, and Part-Of-Speech Tagging

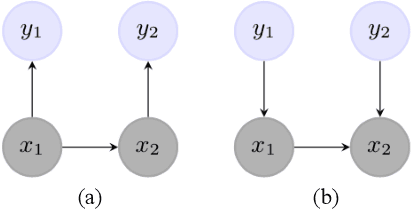
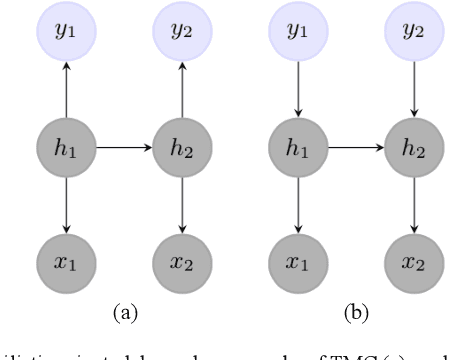
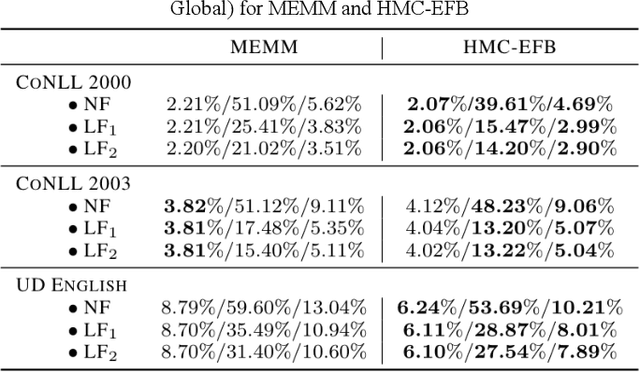
The ability to take into account the characteristics - also called features - of observations is essential in Natural Language Processing (NLP) problems. Hidden Markov Chain (HMC) model associated with classic Forward-Backward probabilities cannot handle arbitrary features like prefixes or suffixes of any size, except with an independence condition. For twenty years, this default has encouraged the development of other sequential models, starting with the Maximum Entropy Markov Model (MEMM), which elegantly integrates arbitrary features. More generally, it led to neglect HMC for NLP. In this paper, we show that the problem is not due to HMC itself, but to the way its restoration algorithms are computed. We present a new way of computing HMC based restorations using original Entropic Forward and Entropic Backward (EFB) probabilities. Our method allows taking into account features in the HMC framework in the same way as in the MEMM framework. We illustrate the efficiency of HMC using EFB in Part-Of-Speech Tagging, showing its superiority over MEMM based restoration. We also specify, as a perspective, how HMCs with EFB might appear as an alternative to Recurrent Neural Networks to treat sequential data with a deep architecture.

A Quadratic Loss Multi-Class SVM

Using a support vector machine requires to set two types of hyperparameters: the soft margin parameter C and the parameters of the kernel. To perform this model selection task, the method of choice is cross-validation. Its leave-one-out variant is known to produce an estimator of the generalization error which is almost unbiased. Its major drawback rests in its time requirement. To overcome this difficulty, several upper bounds on the leave-one-out error of the pattern recognition SVM have been derived. Among those bounds, the most popular one is probably the radius-margin bound. It applies to the hard margin pattern recognition SVM, and by extension to the 2-norm SVM. In this report, we introduce a quadratic loss M-SVM, the M-SVM^2, as a direct extension of the 2-norm SVM to the multi-class case. For this machine, a generalized radius-margin bound is then established.