Using the Naive Bayes as a discriminative classifier

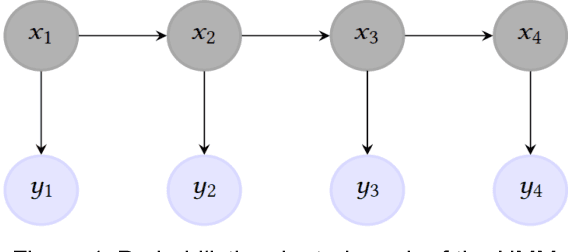
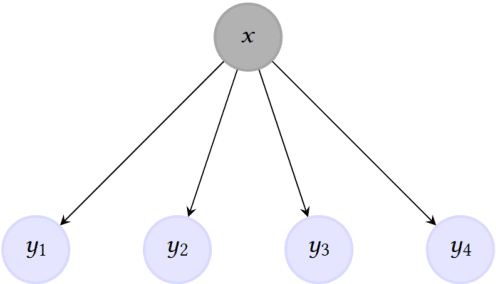
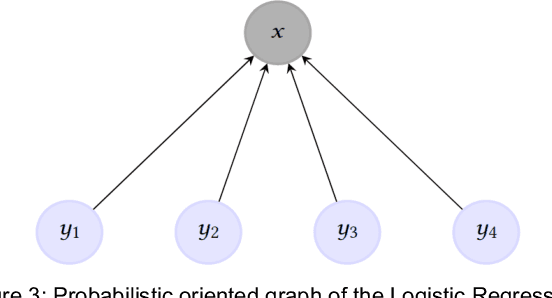
For classification tasks, probabilistic models can be categorized into two disjoint classes: generative or discriminative. It depends on the posterior probability computation of the label $x$ given the observation $y$, $p(x | y)$. On the one hand, generative classifiers, like the Naive Bayes or the Hidden Markov Model (HMM), need the computation of the joint probability $p(x, y)$, before using the Bayes rule to compute $p(x | y)$. On the other hand, discriminative classifiers compute $p(x | y)$ directly, regardless of the observations' law. They are intensively used nowadays, with models as Logistic Regression, Conditional Random Fields (CRF), and Artificial Neural Networks. However, the recent Entropic Forward-Backward algorithm shows that the HMM, considered as a generative model, can also match the discriminative one's definition. This example leads to question if it is the case for other generative models. In this paper, we show that the Naive Bayes classifier can also match the discriminative classifier definition, so it can be used in either a generative or a discriminative way. Moreover, this observation also discusses the notion of Generative-Discriminative pairs, linking, for example, Naive Bayes and Logistic Regression, or HMM and CRF. Related to this point, we show that the Logistic Regression can be viewed as a particular case of the Naive Bayes used in a discriminative way.