A Probabilistic Perspective on Gaussian Filtering and Smoothing
Paper and Code
Jun 08, 2011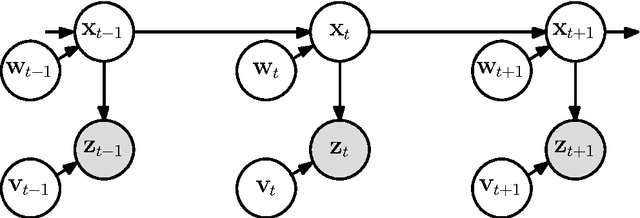
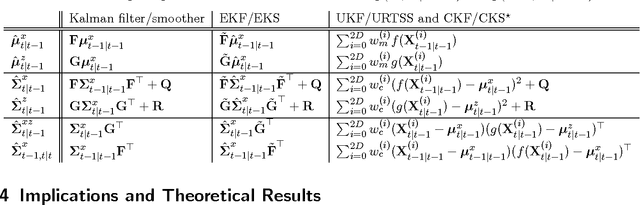
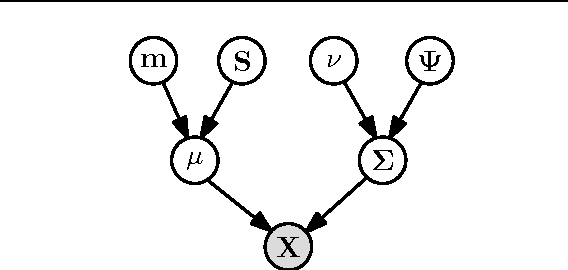

We present a general probabilistic perspective on Gaussian filtering and smoothing. This allows us to show that common approaches to Gaussian filtering/smoothing can be distinguished solely by their methods of computing/approximating the means and covariances of joint probabilities. This implies that novel filters and smoothers can be derived straightforwardly by providing methods for computing these moments. Based on this insight, we derive the cubature Kalman smoother and propose a novel robust filtering and smoothing algorithm based on Gibbs sampling.
* 14 pages. Extended version of conference paper (ACC 2011)
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge