Damping Identification of an Operational Offshore Wind Turbine using Enhanced Kalman filter-based Subspace Identification

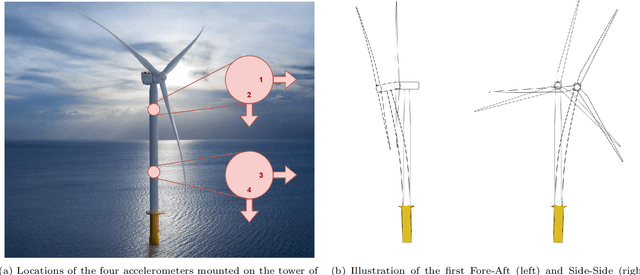
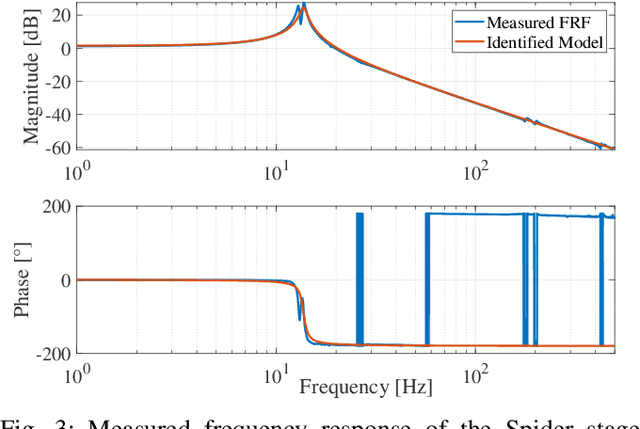
Operational Modal Analysis (OMA) provides essential insights into the structural dynamics of an Offshore Wind Turbine (OWT). In these dynamics, damping is considered an especially important parameter as it governs the magnitude of the response at the natural frequencies. Violation of the stationary white noise excitation requirement of classical OMA algorithms has troubled the identification of operational OWTs due to harmonic excitation caused by rotor rotation. Recently, a novel algorithm was presented that mitigates harmonics by estimating a harmonic subsignal using a Kalman filter and orthogonally removing this signal from the response signal, after which the Stochastic Subspace Identification algorithm is used to identify the system. Although promising results are achieved using this novel algorithm, several shortcomings are still present like the numerical instability of the conventional Kalman filter and the inability to use large or multiple datasets. This paper addresses these shortcomings and applies an enhanced version to a multi-megawatt operational OWT using an economical sensor setup with two accelerometer levels. The algorithm yielded excellent results for the first three tower bending modes with low variance. A comparison of these results against the established time-domain harmonics-mitigating algorithm, Modified LSCE, and the frequency-domain PolyMAX algorithm demonstrated strong agreement in results.

Adaptive Feedforward Control For Reset Feedback Control Systems -- Application in Precision Motion Control

This paper presents a novel adaptive feedforward controller design for reset control systems. The combination of feedforward and reset feedback control promises high performance as the feedforward guarantees reference tracking, while the non-linear feedback element rejects disturbances. To overcome inevitable model mismatches, the feedforward controller adapts to increase precision in reference tracking. Where linear existing adaptive feedforward controllers do not guarantee convergence in the presence of reset, this work presents a novel adaptive law based on converging and diverging regions of adaptation to achieve good tracking. Experimental results demonstrate the claimed advantage of the novel method.

Adaptation of Engineering Wake Models using Gaussian Process Regression and High-Fidelity Simulation Data

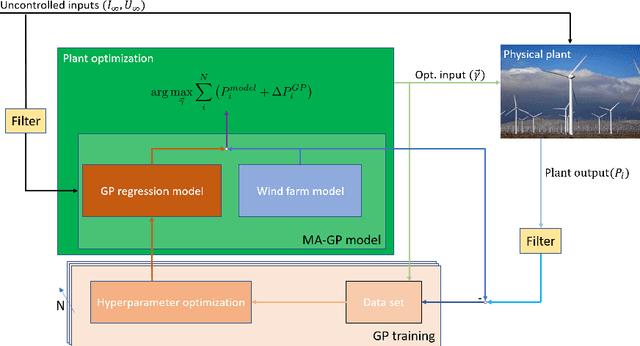
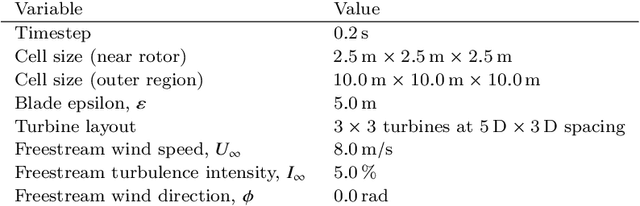
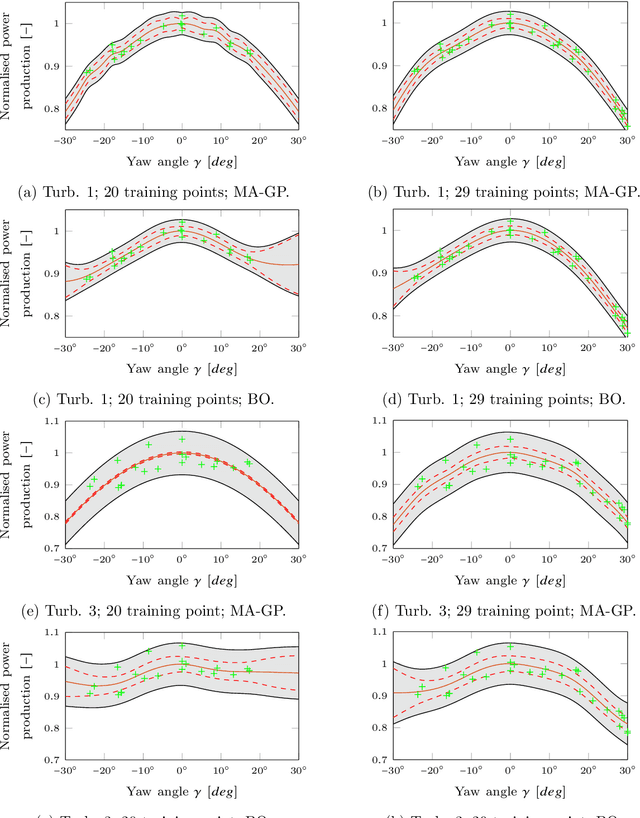
This article investigates the optimization of yaw control inputs of a nine-turbine wind farm. The wind farm is simulated using the high-fidelity simulator SOWFA. The optimization is performed with a modifier adaptation scheme based on Gaussian processes. Modifier adaptation corrects for the mismatch between plant and model and helps to converge to the actual plan optimum. In the case study the modifier adaptation approach is compared with the Bayesian optimization approach. Moreover, the use of two different covariance functions in the Gaussian process regression is discussed. Practical recommendations concerning the data preparation and application of the approach are given. It is shown that both the modifier adaptation and the Bayesian optimization approach can improve the power production with overall smaller yaw misalignments in comparison to the Gaussian wake model.

System Identification through Online Sparse Gaussian Process Regression with Input Noise

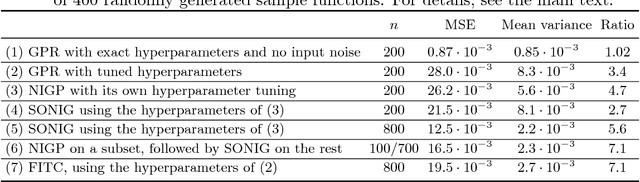
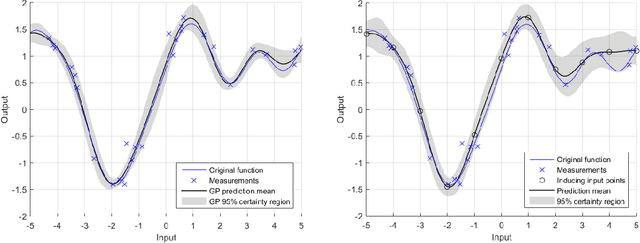
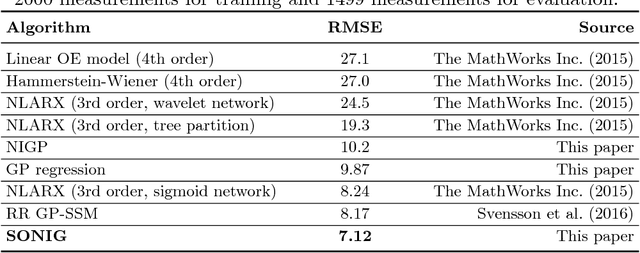
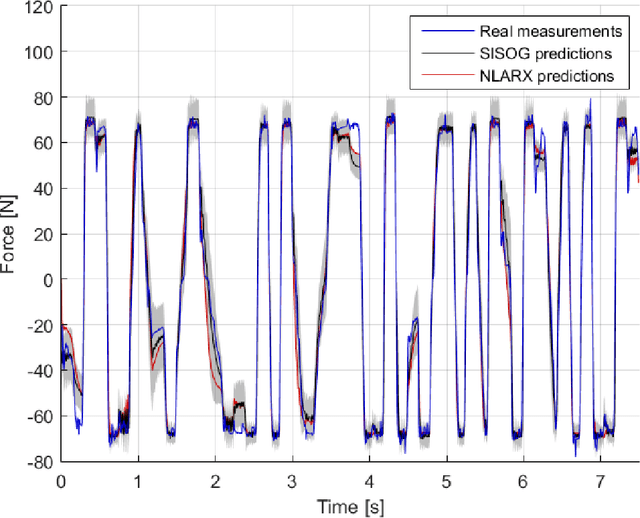
There has been a growing interest in using non-parametric regression methods like Gaussian Process (GP) regression for system identification. GP regression does traditionally have three important downsides: (1) it is computationally intensive, (2) it cannot efficiently implement newly obtained measurements online, and (3) it cannot deal with stochastic (noisy) input points. In this paper we present an algorithm tackling all these three issues simultaneously. The resulting Sparse Online Noisy Input GP (SONIG) regression algorithm can incorporate new noisy measurements in constant runtime. A comparison has shown that it is more accurate than similar existing regression algorithms. When applied to non-linear black-box system modeling, its performance is competitive with existing non-linear ARX models.

A sequential Monte Carlo approach to Thompson sampling for Bayesian optimization

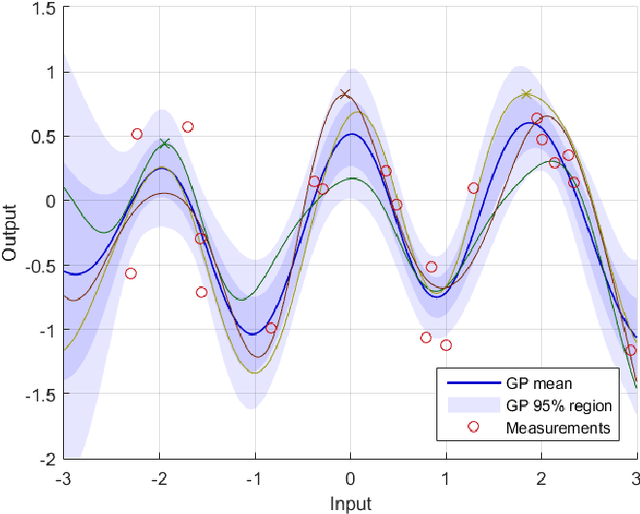
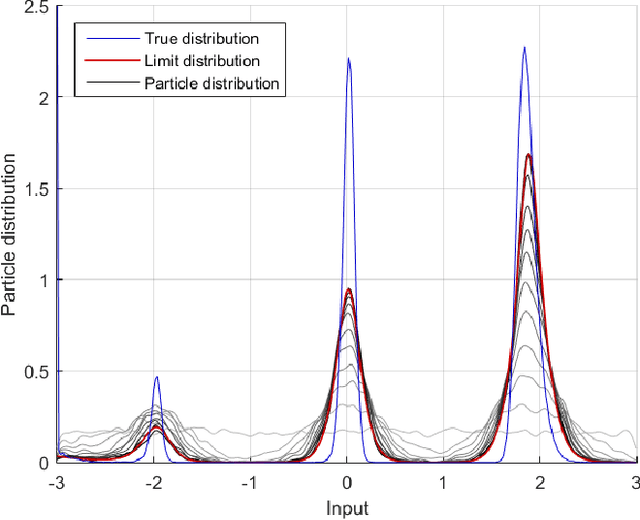
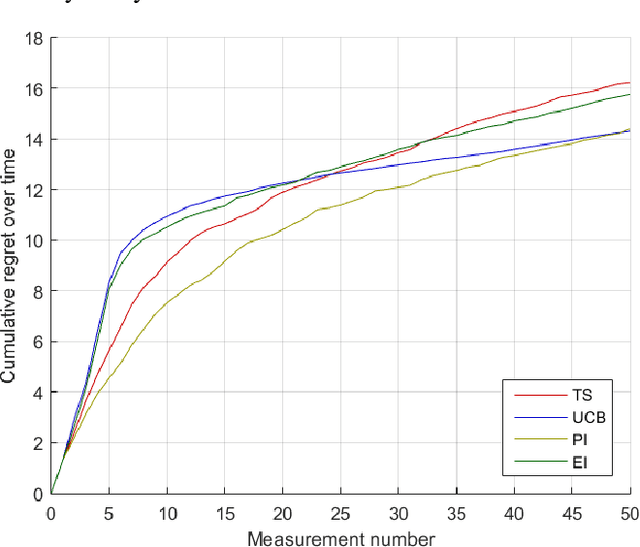
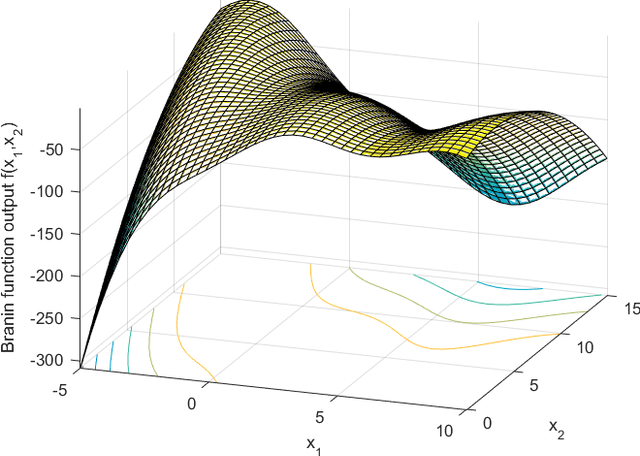
Bayesian optimization through Gaussian process regression is an effective method of optimizing an unknown function for which every measurement is expensive. It approximates the objective function and then recommends a new measurement point to try out. This recommendation is usually selected by optimizing a given acquisition function. After a sufficient number of measurements, a recommendation about the maximum is made. However, a key realization is that the maximum of a Gaussian process is not a deterministic point, but a random variable with a distribution of its own. This distribution cannot be calculated analytically. Our main contribution is an algorithm, inspired by sequential Monte Carlo samplers, that approximates this maximum distribution. Subsequently, by taking samples from this distribution, we enable Thompson sampling to be applied to (armed-bandit) optimization problems with a continuous input space. All this is done without requiring the optimization of a nonlinear acquisition function. Experiments have shown that the resulting optimization method has a competitive performance at keeping the cumulative regret limited.