Tracking student skills real-time through a continuous-variable dynamic Bayesian network

The field of Knowledge Tracing is focused on predicting the success rate of a student for a given skill. Modern methods like Deep Knowledge Tracing provide accurate estimates given enough data, but being based on neural networks they struggle to explain how these estimates are formed. More classical methods like Dynamic Bayesian Networks can do this, but they cannot give data on the accuracy of their estimates and often struggle to incorporate new observations in real-time due to their high computational load. This paper presents a novel method, Performance Distribution Tracing (PDT), in which the distribution of the success rate is traced live. It uses a Dynamic Bayesian Network with continuous random variables as nodes. By tracing the success rate distribution, there is always data available on the accuracy of any success rate estimation. In addition, it makes it possible to combine data from similar/related skills to come up with a more informed estimate of success rates. This makes it possible to predict exercise success rates, providing both explainability and an accuracy indication, even when an exercise requires a combination of different skills to solve. And through the use of the beta distribution functions as conjugate priors, all distributions are available in analytical form, allowing efficient online updates upon new observations. Experiments have shown that the resulting estimates generally feel sufficiently accurate to end-users such that they accept recommendations based on them.

System Identification through Online Sparse Gaussian Process Regression with Input Noise

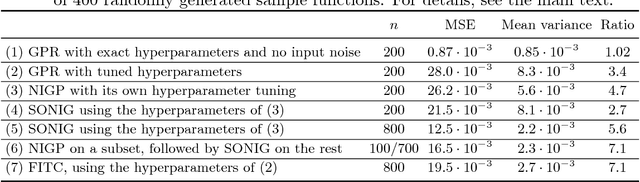
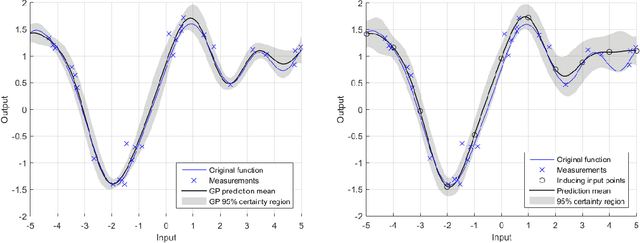
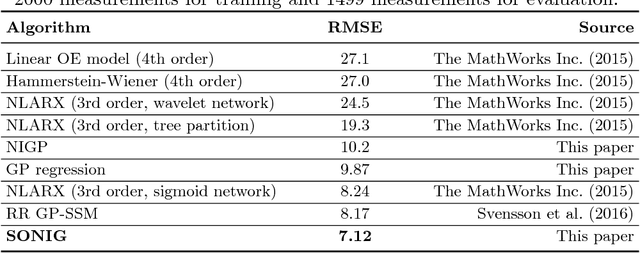
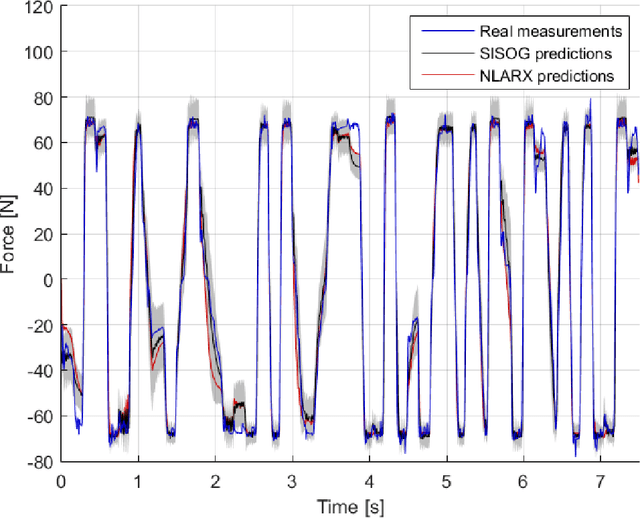
There has been a growing interest in using non-parametric regression methods like Gaussian Process (GP) regression for system identification. GP regression does traditionally have three important downsides: (1) it is computationally intensive, (2) it cannot efficiently implement newly obtained measurements online, and (3) it cannot deal with stochastic (noisy) input points. In this paper we present an algorithm tackling all these three issues simultaneously. The resulting Sparse Online Noisy Input GP (SONIG) regression algorithm can incorporate new noisy measurements in constant runtime. A comparison has shown that it is more accurate than similar existing regression algorithms. When applied to non-linear black-box system modeling, its performance is competitive with existing non-linear ARX models.

A sequential Monte Carlo approach to Thompson sampling for Bayesian optimization

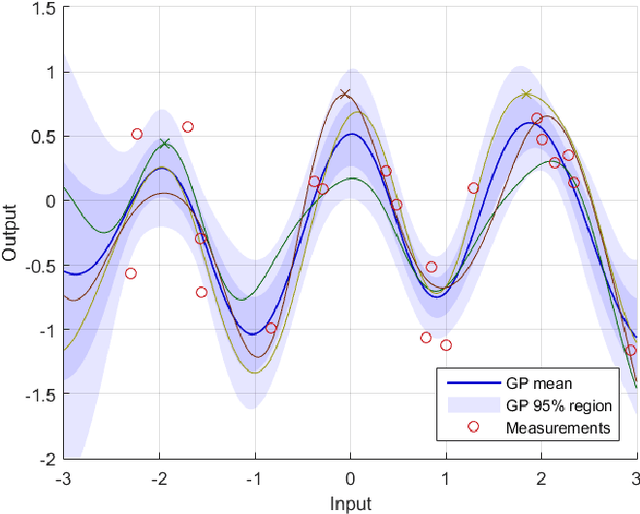
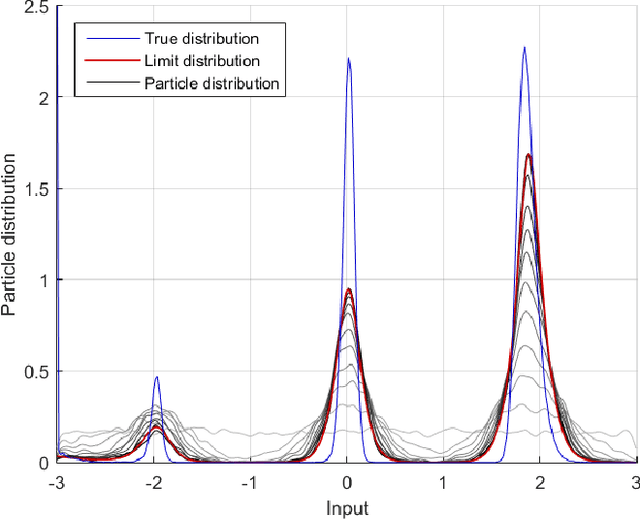
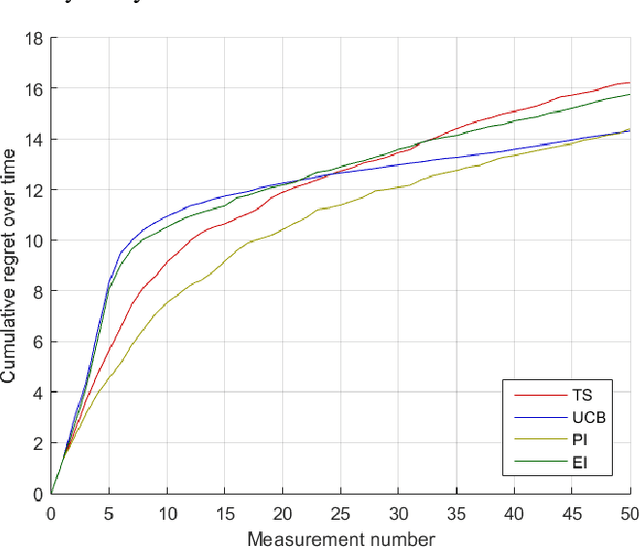
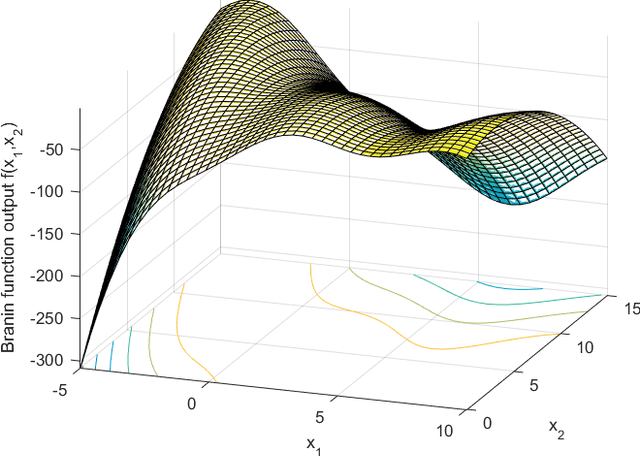
Bayesian optimization through Gaussian process regression is an effective method of optimizing an unknown function for which every measurement is expensive. It approximates the objective function and then recommends a new measurement point to try out. This recommendation is usually selected by optimizing a given acquisition function. After a sufficient number of measurements, a recommendation about the maximum is made. However, a key realization is that the maximum of a Gaussian process is not a deterministic point, but a random variable with a distribution of its own. This distribution cannot be calculated analytically. Our main contribution is an algorithm, inspired by sequential Monte Carlo samplers, that approximates this maximum distribution. Subsequently, by taking samples from this distribution, we enable Thompson sampling to be applied to (armed-bandit) optimization problems with a continuous input space. All this is done without requiring the optimization of a nonlinear acquisition function. Experiments have shown that the resulting optimization method has a competitive performance at keeping the cumulative regret limited.