SNAP: Stopping Catastrophic Forgetting in Hebbian Learning with Sigmoidal Neuronal Adaptive Plasticity

Artificial Neural Networks (ANNs) suffer from catastrophic forgetting, where the learning of new tasks causes the catastrophic forgetting of old tasks. Existing Machine Learning (ML) algorithms, including those using Stochastic Gradient Descent (SGD) and Hebbian Learning typically update their weights linearly with experience i.e., independently of their current strength. This contrasts with biological neurons, which at intermediate strengths are very plastic, but consolidate with Long-Term Potentiation (LTP) once they reach a certain strength. We hypothesize this mechanism might help mitigate catastrophic forgetting. We introduce Sigmoidal Neuronal Adaptive Plasticity (SNAP) an artificial approximation to Long-Term Potentiation for ANNs by having the weights follow a sigmoidal growth behaviour allowing the weights to consolidate and stabilize when they reach sufficiently large or small values. We then compare SNAP to linear weight growth and exponential weight growth and see that SNAP completely prevents the forgetting of previous tasks for Hebbian Learning but not for SGD-base learning.

Articulated Animal AI: An Environment for Animal-like Cognition in a Limbed Agent

This paper presents the Articulated Animal AI Environment for Animal Cognition, an enhanced version of the previous AnimalAI Environment. Key improvements include the addition of agent limbs, enabling more complex behaviors and interactions with the environment that closely resemble real animal movements. The testbench features an integrated curriculum training sequence and evaluation tools, eliminating the need for users to develop their own training programs. Additionally, the tests and training procedures are randomized, which will improve the agent's generalization capabilities. These advancements significantly expand upon the original AnimalAI framework and will be used to evaluate agents on various aspects of animal cognition.

Are Grid Cells Hexagonal for Performance or by Convenience?

This paper investigates whether the hexagonal structure of grid cells provides any performance benefits or if it merely represents a biologically convenient configuration. Utilizing the Vector-HaSH content addressable memory model as a model of the grid cell -- place cell network of the mammalian brain, we compare the performance of square and hexagonal grid cells in tasks of storing and retrieving spatial memories. Our experiments across different path types, path lengths and grid configurations, reveal that hexagonal grid cells perform similarly to square grid cells with respect to spatial representation and memory recall. Our results show comparable accuracy and robustness across different datasets and noise levels on images to recall. These findings suggest that the brain's use of hexagonal grids may be more a matter of biological convenience and ease of implementation rather than because they provide superior performance over square grid cells (which are easier to implement in silico).

A Simple Guard for Learned Optimizers

If the trend of learned components eventually outperforming their hand-crafted version continues, learned optimizers will eventually outperform hand-crafted optimizers like SGD or Adam. Even if learned optimizers (L2Os) eventually outpace hand-crafted ones in practice however, they are still not provably convergent and might fail out of distribution. These are the questions addressed here. Currently, learned optimizers frequently outperform generic hand-crafted optimizers (such as gradient descent) at the beginning of learning but they generally plateau after some time while the generic algorithms continue to make progress and often overtake the learned algorithm as Aesop's tortoise which overtakes the hare and are not. L2Os also still have a difficult time generalizing out of distribution. (Heaton et al., 2020) proposed Safeguarded L2O (GL2O) which can take a learned optimizer and safeguard it with a generic learning algorithm so that by conditionally switching between the two, the resulting algorithm is provably convergent. We propose a new class of Safeguarded L2O, called Loss-Guarded L2O (LGL2O), which is both conceptually simpler and computationally less expensive. The guarding mechanism decides solely based on the expected future loss value of both optimizers. Furthermore, we show theoretical proof of LGL2O's convergence guarantee and empirical results comparing to GL2O and other baselines showing that it combines the best of both L2O and SGD and and in practice converges much better than GL2O.

Combining Reinforcement Learning and Constraint Programming for Combinatorial Optimization

Combinatorial optimization has found applications in numerous fields, from aerospace to transportation planning and economics. The goal is to find an optimal solution among a finite set of possibilities. The well-known challenge one faces with combinatorial optimization is the state-space explosion problem: the number of possibilities grows exponentially with the problem size, which makes solving intractable for large problems. In the last years, deep reinforcement learning (DRL) has shown its promise for designing good heuristics dedicated to solve NP-hard combinatorial optimization problems. However, current approaches have two shortcomings: (1) they mainly focus on the standard travelling salesman problem and they cannot be easily extended to other problems, and (2) they only provide an approximate solution with no systematic ways to improve it or to prove optimality. In another context, constraint programming (CP) is a generic tool to solve combinatorial optimization problems. Based on a complete search procedure, it will always find the optimal solution if we allow an execution time large enough. A critical design choice, that makes CP non-trivial to use in practice, is the branching decision, directing how the search space is explored. In this work, we propose a general and hybrid approach, based on DRL and CP, for solving combinatorial optimization problems. The core of our approach is based on a dynamic programming formulation, that acts as a bridge between both techniques. We experimentally show that our solver is efficient to solve two challenging problems: the traveling salesman problem with time windows, and the 4-moments portfolio optimization problem. Results obtained show that the framework introduced outperforms the stand-alone RL and CP solutions, while being competitive with industrial solvers.

Recurrent Ladder Networks

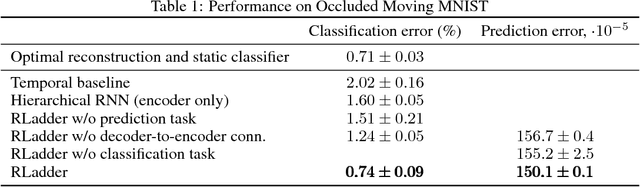
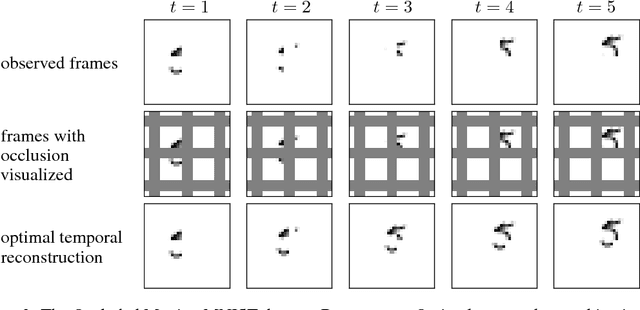
We propose a recurrent extension of the Ladder networks whose structure is motivated by the inference required in hierarchical latent variable models. We demonstrate that the recurrent Ladder is able to handle a wide variety of complex learning tasks that benefit from iterative inference and temporal modeling. The architecture shows close-to-optimal results on temporal modeling of video data, competitive results on music modeling, and improved perceptual grouping based on higher order abstractions, such as stochastic textures and motion cues. We present results for fully supervised, semi-supervised, and unsupervised tasks. The results suggest that the proposed architecture and principles are powerful tools for learning a hierarchy of abstractions, learning iterative inference and handling temporal information.