MAP-Elites with Descriptor-Conditioned Gradients and Archive Distillation into a Single Policy

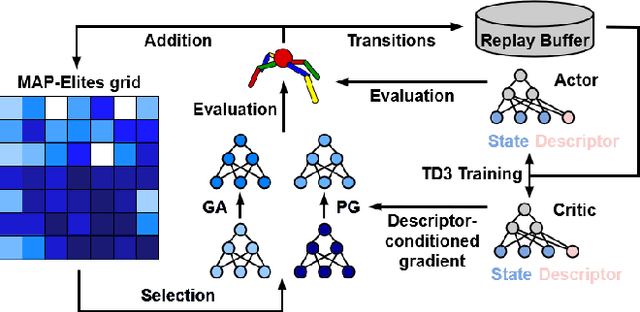
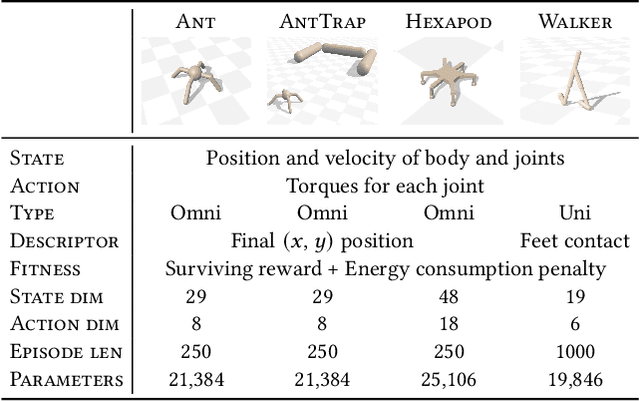
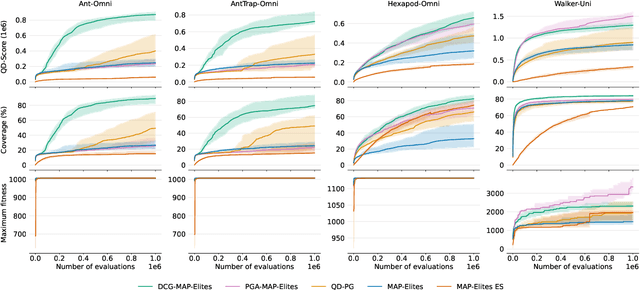
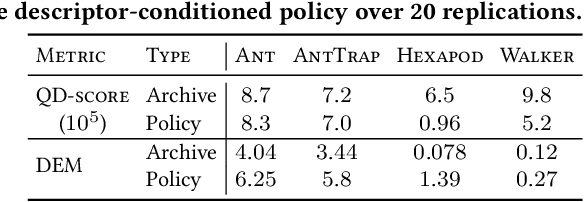
Quality-Diversity algorithms, such as MAP-Elites, are a branch of Evolutionary Computation generating collections of diverse and high-performing solutions, that have been successfully applied to a variety of domains and particularly in evolutionary robotics. However, MAP-Elites performs a divergent search based on random mutations originating from Genetic Algorithms, and thus, is limited to evolving populations of low-dimensional solutions. PGA-MAP-Elites overcomes this limitation by integrating a gradient-based variation operator inspired by Deep Reinforcement Learning which enables the evolution of large neural networks. Although high-performing in many environments, PGA-MAP-Elites fails on several tasks where the convergent search of the gradient-based operator does not direct mutations towards archive-improving solutions. In this work, we present two contributions: (1) we enhance the Policy Gradient variation operator with a descriptor-conditioned critic that improves the archive across the entire descriptor space, (2) we exploit the actor-critic training to learn a descriptor-conditioned policy at no additional cost, distilling the knowledge of the archive into one single versatile policy that can execute the entire range of behaviors contained in the archive. Our algorithm, DCG-MAP-Elites improves the QD score over PGA-MAP-Elites by 82% on average, on a set of challenging locomotion tasks.

SeaPearl: A Constraint Programming Solver guided by Reinforcement Learning

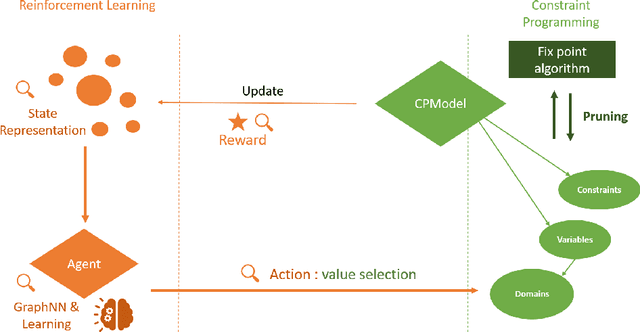
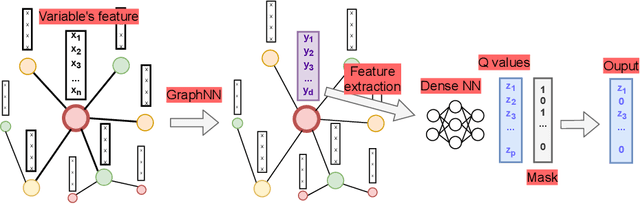
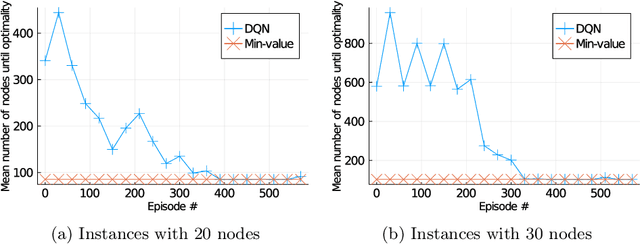
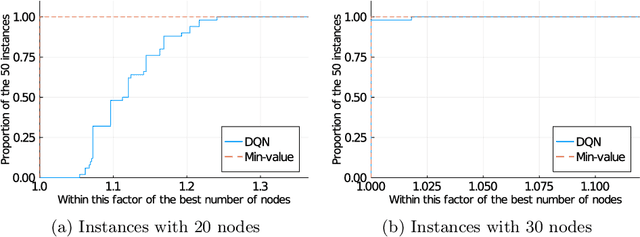
The design of efficient and generic algorithms for solving combinatorial optimization problems has been an active field of research for many years. Standard exact solving approaches are based on a clever and complete enumeration of the solution set. A critical and non-trivial design choice with such methods is the branching strategy, directing how the search is performed. The last decade has shown an increasing interest in the design of machine learning-based heuristics to solve combinatorial optimization problems. The goal is to leverage knowledge from historical data to solve similar new instances of a problem. Used alone, such heuristics are only able to provide approximate solutions efficiently, but cannot prove optimality nor bounds on their solution. Recent works have shown that reinforcement learning can be successfully used for driving the search phase of constraint programming (CP) solvers. However, it has also been shown that this hybridization is challenging to build, as standard CP frameworks do not natively include machine learning mechanisms, leading to some sources of inefficiencies. This paper presents the proof of concept for SeaPearl, a new CP solver implemented in Julia, that supports machine learning routines in order to learn branching decisions using reinforcement learning. Support for modeling the learning component is also provided. We illustrate the modeling and solution performance of this new solver on two problems. Although not yet competitive with industrial solvers, SeaPearl aims to provide a flexible and open-source framework in order to facilitate future research in the hybridization of constraint programming and machine learning.