Using Formal Models, Safety Shields and Certified Control to Validate AI-Based Train Systems

The certification of autonomous systems is an important concern in science and industry. The KI-LOK project explores new methods for certifying and safely integrating AI components into autonomous trains. We pursued a two-layered approach: (1) ensuring the safety of the steering system by formal analysis using the B method, and (2) improving the reliability of the perception system with a runtime certificate checker. This work links both strategies within a demonstrator that runs simulations on the formal model, controlled by the real AI output and the real certificate checker. The demonstrator is integrated into the validation tool ProB. This enables runtime monitoring, runtime verification, and statistical validation of formal safety properties using a formal B model. Consequently, one can detect and analyse potential vulnerabilities and weaknesses of the AI and the certificate checker. We apply these techniques to a signal detection case study and present our findings.

Certified Control for Train Sign Classification

There is considerable industrial interest in integrating AI techniques into railway systems, notably for fully autonomous train systems. The KI-LOK research project is involved in developing new methods for certifying such AI-based systems. Here we explore the utility of a certified control architecture for a runtime monitor that prevents false positive detection of traffic signs in an AI-based perception system. The monitor uses classical computer vision algorithms to check if the signs -- detected by an AI object detection model -- fit predefined specifications. We provide such specifications for some critical signs and integrate a Python prototype of the monitor with a popular object detection model to measure relevant performance metrics on generated data. Our initial results are promising, achieving considerable precision gains with only minor recall reduction; however, further investigation into generalization possibilities will be necessary.

Knowledge Representation Analysis of Graph Mining

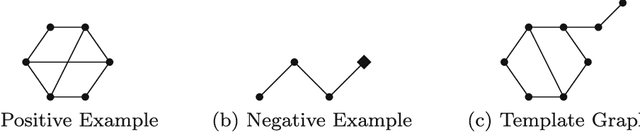
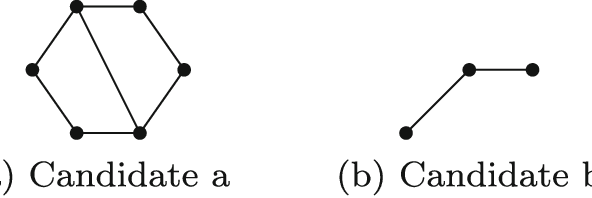
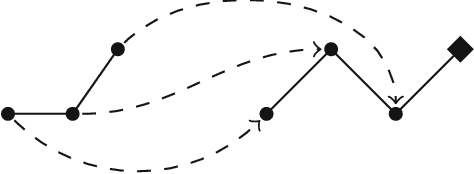
Many problems, especially those with a composite structure, can naturally be expressed in higher order logic. From a KR perspective modeling these problems in an intuitive way is a challenging task. In this paper we study the graph mining problem as an example of a higher order problem. In short, this problem asks us to find a graph that frequently occurs as a subgraph among a set of example graphs. We start from the problem's mathematical definition to solve it in three state-of-the-art specification systems. For IDP and ASP, which have no native support for higher order logic, we propose the use of encoding techniques such as the disjoint union technique and the saturation technique. ProB benefits from the higher order support for sets. We compare the performance of the three approaches to get an idea of the overhead of the higher order support. We propose higher-order language extensions for IDP-like specification languages and discuss what kind of solver support is needed. Native higher order shifts the burden of rewriting specifications using encoding techniques from the user to the solver itself.

Offline Specialisation in Prolog Using a Hand-Written Compiler Generator

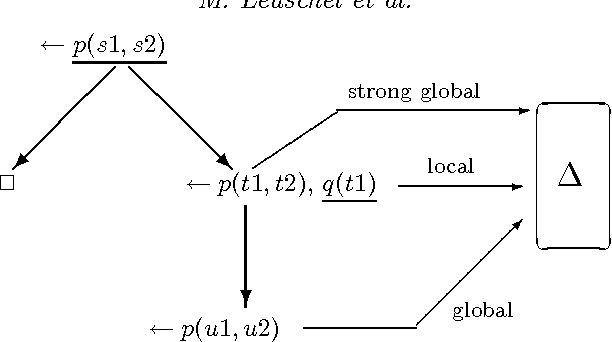
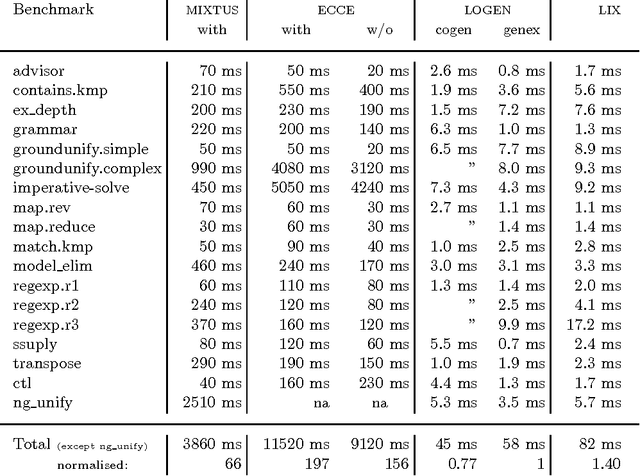
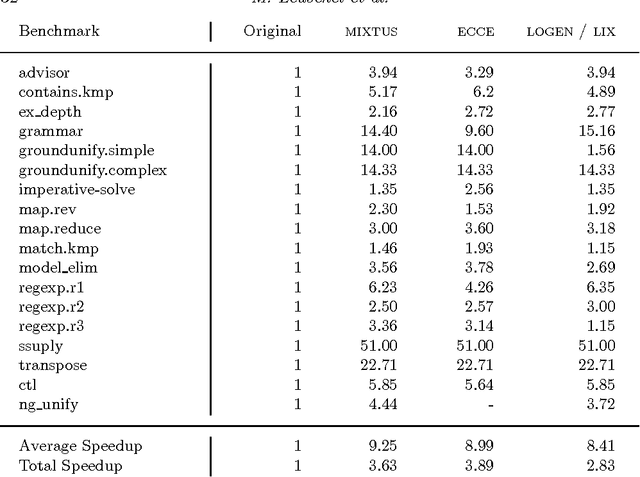
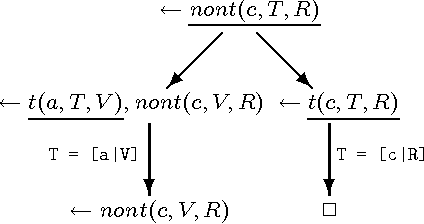
The so called ``cogen approach'' to program specialisation, writing a compiler generator instead of a specialiser, has been used with considerable success in partial evaluation of both functional and imperative languages. This paper demonstrates that the cogen approach is also applicable to the specialisation of logic programs (also called partial deduction) and leads to effective specialisers. Moreover, using good binding-time annotations, the speed-ups of the specialised programs are comparable to the speed-ups obtained with online specialisers. The paper first develops a generic approach to offline partial deduction and then a specific offline partial deduction method, leading to the offline system LIX for pure logic programs. While this is a usable specialiser by itself, it is used to develop the cogen system LOGEN. Given a program, a specification of what inputs will be static, and an annotation specifying which calls should be unfolded, LOGEN generates a specialised specialiser for the program at hand. Running this specialiser with particular values for the static inputs results in the specialised program. While this requires two steps instead of one, the efficiency of the specialisation process is improved in situations where the same program is specialised multiple times. The paper also presents and evaluates an automatic binding-time analysis that is able to derive the annotations. While the derived annotations are still suboptimal compared to hand-crafted ones, they enable non-expert users to use the LOGEN system in a fully automated way. Finally, LOGEN is extended so as to directly support a large part of Prolog's declarative and non-declarative features and so as to be able to perform so called mixline specialisations.

Logic program specialisation through partial deduction: Control issues

Program specialisation aims at improving the overall performance of programs by performing source to source transformations. A common approach within functional and logic programming, known respectively as partial evaluation and partial deduction, is to exploit partial knowledge about the input. It is achieved through a well-automated application of parts of the Burstall-Darlington unfold/fold transformation framework. The main challenge in developing systems is to design automatic control that ensures correctness, efficiency, and termination. This survey and tutorial presents the main developments in controlling partial deduction over the past 10 years and analyses their respective merits and shortcomings. It ends with an assessment of current achievements and sketches some remaining research challenges.