Knowledge Representation Analysis of Graph Mining
Paper and Code
Aug 31, 2016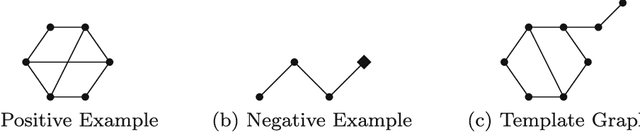
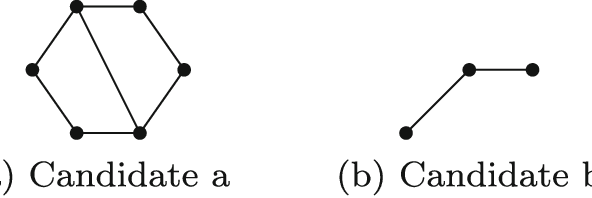

Many problems, especially those with a composite structure, can naturally be expressed in higher order logic. From a KR perspective modeling these problems in an intuitive way is a challenging task. In this paper we study the graph mining problem as an example of a higher order problem. In short, this problem asks us to find a graph that frequently occurs as a subgraph among a set of example graphs. We start from the problem's mathematical definition to solve it in three state-of-the-art specification systems. For IDP and ASP, which have no native support for higher order logic, we propose the use of encoding techniques such as the disjoint union technique and the saturation technique. ProB benefits from the higher order support for sets. We compare the performance of the three approaches to get an idea of the overhead of the higher order support. We propose higher-order language extensions for IDP-like specification languages and discuss what kind of solver support is needed. Native higher order shifts the burden of rewriting specifications using encoding techniques from the user to the solver itself.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge