Grounding FO and FO(ID) with Bounds

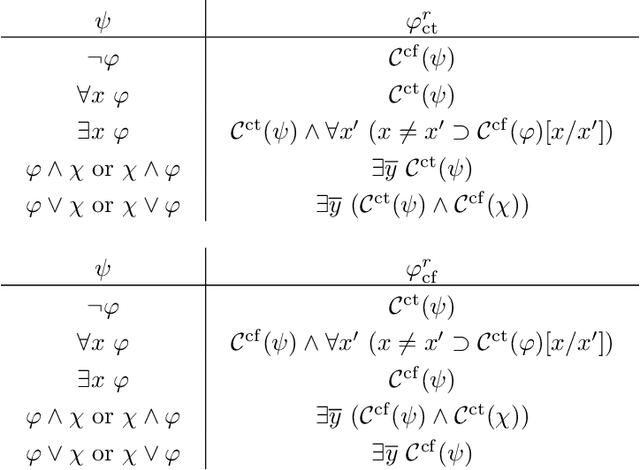
Grounding is the task of reducing a first-order theory and finite domain to an equivalent propositional theory. It is used as preprocessing phase in many logic-based reasoning systems. Such systems provide a rich first-order input language to a user and can rely on efficient propositional solvers to perform the actual reasoning. Besides a first-order theory and finite domain, the input for grounders contains in many applications also additional data. By exploiting this data, the size of the grounders output can often be reduced significantly. A common practice to improve the efficiency of a grounder in this context is by manually adding semantically redundant information to the input theory, indicating where and when the grounder should exploit the data. In this paper we present a method to compute and add such redundant information automatically. Our method therefore simplifies the task of writing input theories that can be grounded efficiently by current systems. We first present our method for classical first-order logic (FO) theories. Then we extend it to FO(ID), the extension of FO with inductive definitions, which allows for more concise and comprehensive input theories. We discuss implementation issues and experimentally validate the practical applicability of our method.

LPC: A Sequent Calculus Proof System for Propositional Logic Extended with Inductive Definitions

The logic FO(ID) uses ideas from the field of logic programming to extend first order logic with non-monotone inductive definitions. Such logic formally extends logic programming, abductive logic programming and datalog, and thus formalizes the view on these formalisms as logics of (generalized) inductive definitions. The goal of this paper is to study a deductive inference method for PC(ID), which is the propositional fragment of FO(ID). We introduce a formal proof system based on the sequent calculus (Gentzen-style deductive system) for this logic. As PC(ID) is an integration of classical propositional logic and propositional inductive definitions, our sequent calculus proof system integrates inference rules for propositional calculus and definitions. We present the soundness and completeness of this proof system with respect to a slightly restricted fragment of PC(ID). We also provide some complexity results for PC(ID). By developing the proof system for PC(ID), it helps us to enhance the understanding of proof-theoretic foundations of FO(ID), and therefore to investigate useful proof systems for FO(ID).

A prototype of a knowledge-based programming environment

In this paper we present a proposal for a knowledge-based programming environment. In such an environment, declarative background knowledge, procedures, and concrete data are represented in suitable languages and combined in a flexible manner. This leads to a highly declarative programming style. We illustrate our approach on an example and report about our prototype implementation.

Constraint Propagation for First-Order Logic and Inductive Definitions

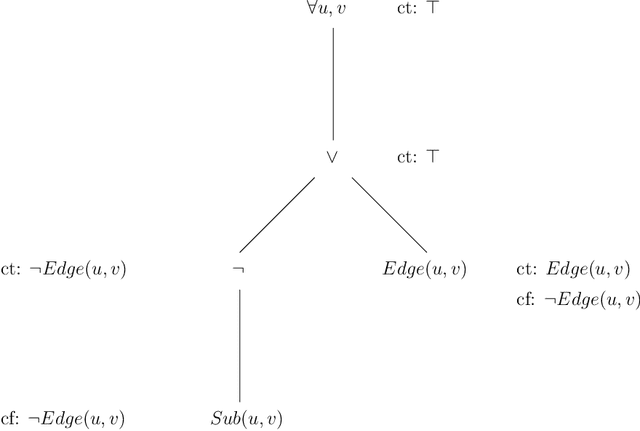
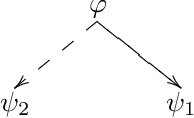
Constraint propagation is one of the basic forms of inference in many logic-based reasoning systems. In this paper, we investigate constraint propagation for first-order logic (FO), a suitable language to express a wide variety of constraints. We present an algorithm with polynomial-time data complexity for constraint propagation in the context of an FO theory and a finite structure. We show that constraint propagation in this manner can be represented by a datalog program and that the algorithm can be executed symbolically, i.e., independently of a structure. Next, we extend the algorithm to FO(ID), the extension of FO with inductive definitions. Finally, we discuss several applications.